Was ist darstellende Geometrie?
Inhaltsverzeichnis
Nach Wegen, den Raum auf verständliche und geordnete Weise genau darzustellen, hat die Menschheit seit Anbeginn der Zeit gesucht. Einfache Zeichnungen oder Diagramme dienten seit der Antike, doch erst die Arbeiten Gaspard Monges im 18. Jahrhundert verliehen diesen Bemühungen mathematische Präzision und Allgemeingültigkeit. Die Darstellende Geometrie ist die Wissenschaft von der exakten und übersichtlichen Abbildung von Raumobjekten auf zweidimensionale Ebenen.
Was ist die Grundlage der darstellenden Geometrie?
Dass Projektionen auf Ebenen komplexe dreidimensionale Körper darstellen können, ist die zentrale Idee der Darstellenden Geometrie. Dies ermöglicht die Analyse ihrer Struktur und räumlichen Beziehungen, während man sich im Bereich zweidimensionaler Zeichnungen bewegt. Dieser Ansatz ist von großer Bedeutung für Ingenieurwesen und Architektur, wo es oft entscheidend ist, die Struktur eines Gebäudes oder einer Maschine präzise zu planen, bevor man mit der Umsetzung beginnt.
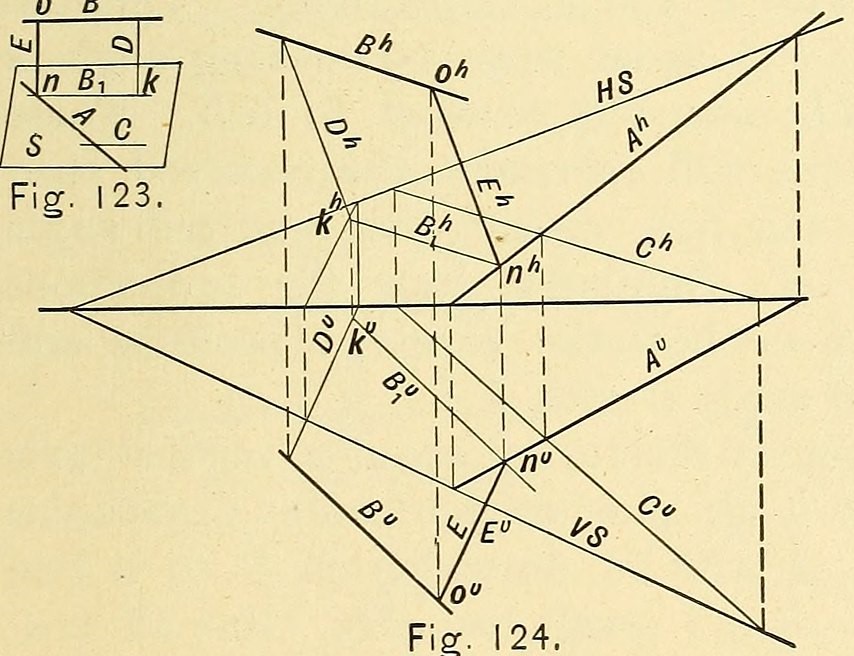
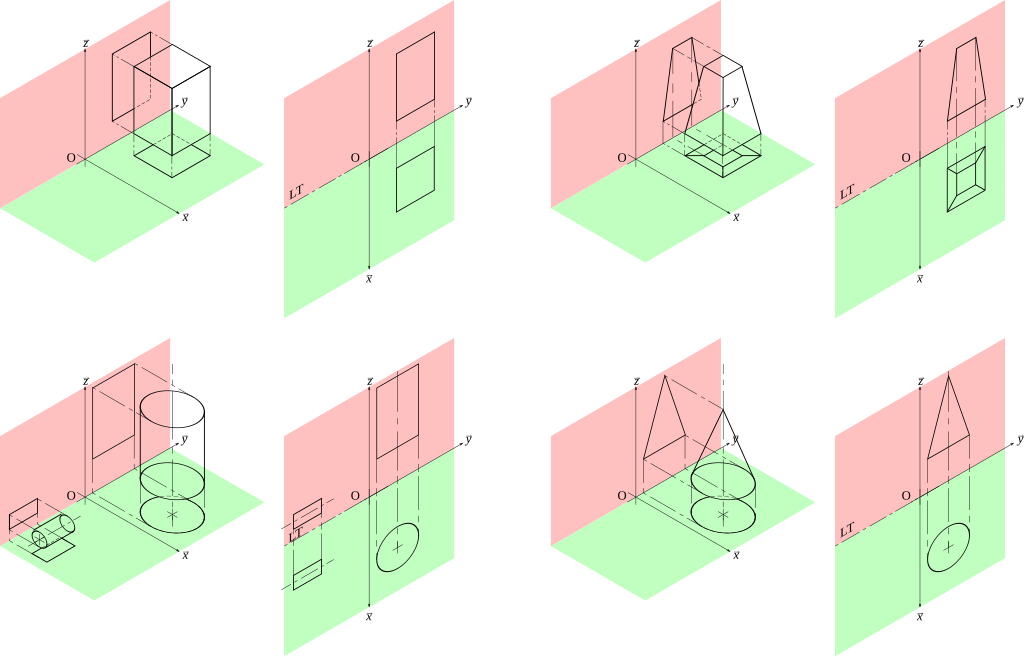
Mit Hilfe der Darstellenden Geometrie wird der Raum auf einfache Weise begreifbar gemacht. Mit Hilfe der rechtwinkligen Projektion, einer der grundlegenden Techniken dieser Disziplin, ist die Betrachtung eines Körpers aus verschiedenen Perspektiven möglich, was diese Methode zu einem äußerst vielseitigen Werkzeug macht. Ein Bild, das von oben (horizontale Projektion), von der Seite (seitliche Projektion) oder von vorne (vertikale Projektion) aufgenommen wird, erfasst viele Informationen über ein Objekt, die in einem Designkontext analysiert werden können.
Ihr Vorteil besteht darin, dass sie theoretische Mathematik mit praktischen Anwendungen verknüpfen können. Die Fähigkeit, vorherzusagen, wie die verschiedenen Elemente in der Realität zusammenwirken, ist die Grundlage für die Planung von Gebäuden, Brücken oder Maschinen. Mit Hilfe der Methoden von Monge waren die Ingenieure in der Lage, Bauprobleme bereits vor Beginn der Arbeiten auf der Baustelle zu planen und zu lösen.
Entstehung und Entwicklung der Disziplin
Obwohl die darstellende Geometrie heute als grundlegender Zweig der angewandten Mathematik gilt, verdankt sie ihre Entstehung praktischen Bedürfnissen. Im 18. Jahrhundert, als Gaspard Monge seine Karriere als junger Militäringenieur begann, stieß er auf ein Problem, das eine genaue Modellierung des Raums im Zusammenhang mit der Planung von Befestigungsanlagen erforderte. Sie mussten mit großer Präzision gebaut und mit bombensicheren Wänden und Gewölben versehen werden.
Im Alter von 18 Jahren hatte Monge bereits die Grundlagen eines Systems entwickelt, mit dem komplexe dreidimensionale Objekte in zwei Dimensionen dargestellt werden konnten. Aufgrund der strategischen Bedeutung dieses Wissens galten seine Entdeckungen jedoch als militärisches Geheimnis und wurden viele Jahre lang nicht der Öffentlichkeit zugänglich gemacht. Erst 1794, nach der Französischen Revolution, gab Monge sein Wissen weiter und führte die Entwässerungsgeometrie in den Lehrplan der École Normale und der neu gegründeten École Polytechnique ein.
Als 1795 an der École Polytechnique die Geometrie des Zeichnens eingeführt wurde, setzte Monge einen Meilenstein. Parallel zu seinen herausragenden mathematischen Fähigkeiten besaß Monge die Gabe, komplexe Ideen auf verständliche und inspirierende Weise zu vermitteln. Schon in seinen ersten Vorlesungen wurde das neue Fach von den Studierenden mit großem Interesse aufgenommen und wurde zur Grundlage der technischen Wissenschaften.
Monge definierte die Zeichnergeometrie als ein Werkzeug mit zwei Hauptzielen: erstens die präzise Darstellung dreidimensionaler Objekte in zwei Dimensionen und zweitens das Ziehen von Schlussfolgerungen über die Formen und Beziehungen zwischen diesen Objekten. Diese Prinzipien waren die Grundlage für die theoretische und praktische Bedeutung der neuen Disziplin und für deren rasche Verbreitung.

Grundlegende Konzepte der Zeichnergeometrie
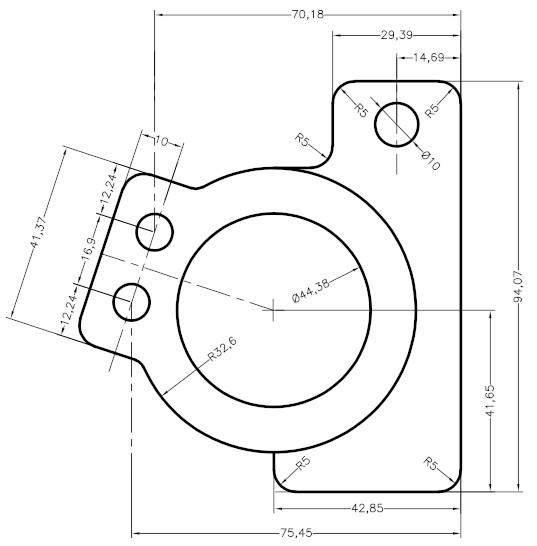
Rechtwinklige Projektionen, mit denen dreidimensionale Objekte auf einer ebenen Fläche übersichtlich dargestellt werden können, sind das zentrale Element der Zeichnungsgeometrie. Mit Hilfe dieser Technik ist die Erstellung von Zeichnungen mit verschiedenen Ansichten eines Objekts möglich: von oben, von vorne und von der Seite. Jede Projektion zeigt verschiedene Aspekte des Bauwerks, wodurch die Geometrie des Bauwerks besser verstanden werden kann.
Rechteckige Projektionen beispielsweise sind im Bauwesen sehr praktisch. Der Grundriss eines Gebäudes zeigt die Anordnung der Räume und die Anordnung der Türen und Fenster, während vertikale Projektionen die Höhe und Proportionen der Fassade zeigen. Darüber hinaus ermöglichen Seitenprojektionen die Analyse der Tiefe und der Details der Struktur, wie z. B. Dachvorsprünge oder Fassadendetails.
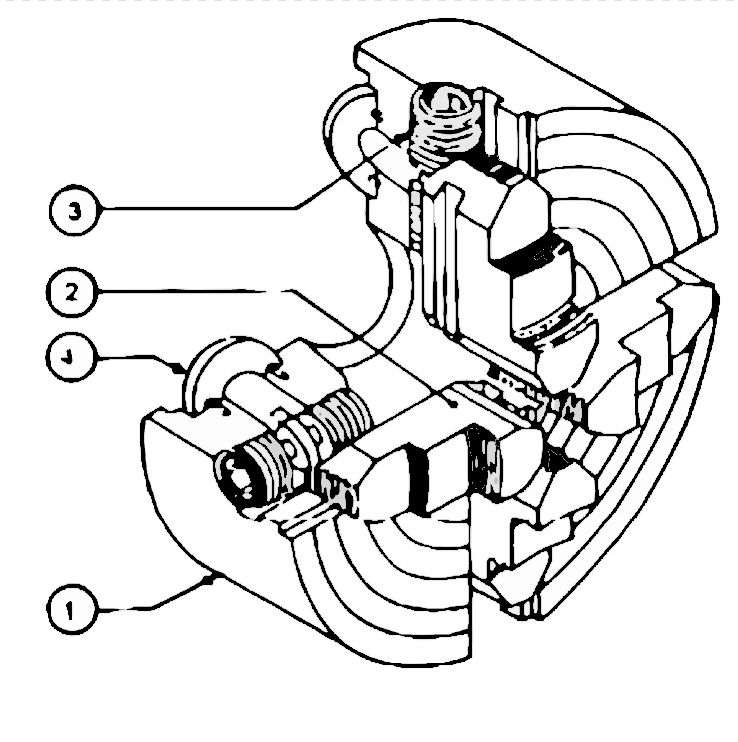
Mit Hilfe der Zeichnungsgeometrie können auch komplexe räumliche Probleme gelöst werden, wie z.B. die Durchdringung von Festkörpern. In der Architektur wird diese Technik verwendet, um gewölbte Dächer zu entwerfen und zu zeigen, wie die einzelnen Elemente ineinandergreifen. Im Maschinenbau findet es Anwendung bei der Konstruktion von Maschinenteilen, bei denen die einzelnen Komponenten perfekt aufeinander abgestimmt sein müssen.
Vielseitigkeit ist ein wesentliches Merkmal der Zeichengeometrie. Mit Hilfe der Projektionsmethode können Bilder sowohl von einfachen geometrischen Figuren als auch von komplexen Formen wie z. B. ellipsoiden oder hyperbolischen Flächen erzeugt werden. Die Einführung dieser Technik in die Designpraxis war der unschätzbare Beitrag von Gaspard Monge, der die Zeichnungsgeometrie zu einem Werkzeug machte, das mathematische Präzision mit Ästhetik und Funktionalität verbindet.
Auch die Visualisierung von Konzepten, die zuvor nur in der Vorstellung existierten, wurde durch die Entwurfsgeometrie möglich. Diese Techniken sind nicht nur ein Werkzeug zur Erstellung von Zeichnungen, sondern auch ein Werkzeug zur räumlichen Analyse, um Entwürfe zu verstehen und zu optimieren.
Monge’s Anwendungen und Innovationen
Eine der beeindruckendsten Leistungen von Gaspard Monge war die Anwendung der Prinzipien der Entwurfsgeometrie auf die Lösung praktischer Konstruktionsprobleme. Zu seinen Arbeiten gehörten nicht nur theoretische Raummodelle, sondern auch spezifische Ingenieurtechniken wie die Stereotomie – die Wissenschaft des Steinhauens, deren Anwendung auf Wölbungen und mörtelloses Bauen die Architektur des 18. Jahrhunderts revolutionierte.
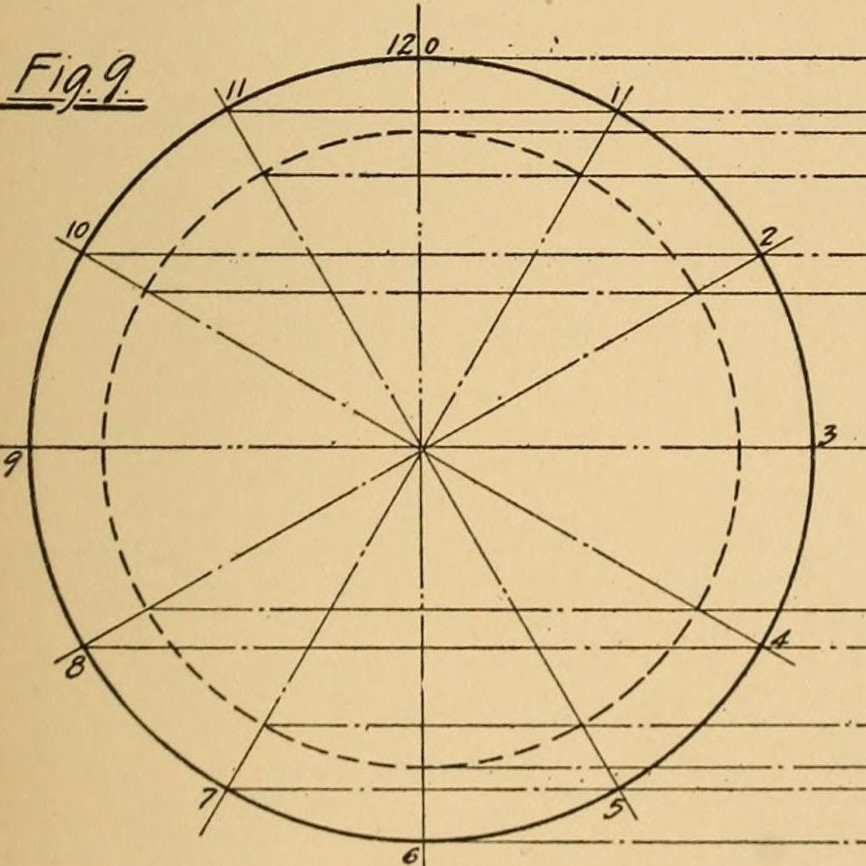
Monge erkannte, dass das richtige Verständnis der Krümmungen auf der Oberfläche eines Gegenstandes eine wesentliche Voraussetzung für erfolgreiches Design ist. Diese Linien – eine orthogonale Anordnung auf der Oberfläche – heben den Charakter des Objekts in ästhetischer Hinsicht hervor und erleichtern vor allem die Planung der Verteilung der Strukturelemente. Diese Prinzipien ermöglichten es, Steingewölbe aus präzise aufeinander abgestimmten Elementen zusammenzusetzen, die ohne Verwendung von Mörtel stabile Strukturen bildeten.
Nicht nur auf architektonische Strukturen beschränkte sich Monges Innovation. Auch im Maschinenbau, wo die Präzision der Konstruktion von entscheidender Bedeutung ist, wurden seine Methoden angewandt. Durch die Anwendung der Rechteckprojektion im Maschinenbau wurde eine genaue Festlegung der Formen und Proportionen der einzelnen Teile und ihrer Passung möglich.
Ein weiterer Durchbruch war die Verbindung von Konstruktionsgeometrie und Ästhetik. Monge vertrat die Auffassung, dass konstruktive Linien den Charakter der Oberfläche wiedergeben müssen, auf der sie liegen. Damit führte er mit der gegenseitigen Ergänzung von Form und Funktion eine neue Qualität in die architektonische Gestaltung ein. Die Trennlinien, die sich an den Gewölben oder an den Fassaden der Gebäude befinden, werden zu einem dekorativen Element, das dem Ganzen ein harmonisches Aussehen verleiht.
Monge hat gezeigt, dass die Geometrie des Zeichners nicht nur ein mathematisches Werkzeug ist, sondern eine universelle Sprache, die es ermöglicht, die theoretischen Grundlagen mit den praktischen Erfordernissen der Konstruktion und des Designs zu verbinden. Aus diesem Grund sind seine Arbeiten auch heute noch von Bedeutung und eine Inspirationsquelle für nachfolgende Generationen von Designern.
Kritik und Einfluss der Entwurfsgeometrie
Trotz ihrer bahnbrechenden Eigenschaften und ihrer vielfältigen Anwendungsmöglichkeiten war die Theorie Gaspard Monges nicht frei von Einschränkungen und Kritik, vor allem in Bezug auf komplexe Strukturen: ‚Die Geometrie, die wir heute kennen, ist nicht nur eine Theorie, sondern auch eine Praxis. Die Schwierigkeit, die Prinzipien der Stereotomie auf Strukturen mit ungewöhnlicheren Formen wie diagonale Brücken oder Gewölbe mit nicht dehnbaren Oberflächen anzuwenden, war das erste und auffälligste Problem.
Ein Beispiel für diese Einschränkungen waren Brücken, die im 19. Jahrhundert in Europa gebaut wurden, insbesondere Bauwerke, die für den Zugverkehr ausgelegt waren. Bei schrägen Brücken, bei denen der Winkel zwischen Straße und Schiene gering war, bot die Entwurfsgeometrie von Monge nicht immer geeignete Werkzeuge für eine optimale Kraftverteilung. Wie Kritiker betonten, entsprachen die von Monge als zentrales Gestaltungselement vorgeschlagenen Krümmungslinien nicht immer den tatsächlichen mechanischen Anforderungen, wie z. B. Druckverteilung oder Vibrationsfestigkeit.
Diese durchaus berechtigte Kritik schmälert jedoch nicht die Bedeutung Monges als Begründer der grundlegenden Methodik der Raumgeometrie. Sein Werk hat Generationen von Ingenieuren angeregt, seine Methoden weiterzuentwickeln und neuen technischen Herausforderungen anzupassen. Beispielsweise wurden die Konstruktionstechniken durch die Entwicklung der Elastizitätstheorie und der Materialwissenschaften, die ein besseres Verständnis des komplexen mechanischen Verhaltens von Strukturen ermöglichten, in der zweiten Hälfte des 19 Jahrhunderst.
Monge hatte auch Einfluss auf die spätere Entwicklung der Architektur und des Ingenieurwesens im 20. Jahrhundert. In der Moderne eröffneten Strukturen wie Betonschalen und leichte Stahlkonstruktionen völlig neue Gestaltungsmöglichkeiten, basierten aber gleichzeitig auf den Grundprinzipien der Entwurfsgeometrie. Monge legte mit seinen Ideen, die Theorie und Praxis verbanden, den Grundstein für die Entwicklung dieser innovativen Technologien.
Monge hat auch die technische Ausbildung nachhaltig geprägt. Sein Ansatz, der die praktische Anwendung der Geometrie betont, wurde weltweit in technischen Schulen übernommen. Seine Unterrichtsmethode, die auf einer klaren Darstellung der Beziehung von Raumkörpern und ihrer Projektion beruht, wurde zur Grundlage der Ingenieur- und Architektenausbildung.
Zusammenfassend lässt sich sagen, dass die Kritik an einigen Aspekten von Monges Theorie ein Ausgangspunkt für die Weiterentwicklung der Entwurfsgeometrie war und nicht deren Ablehnung. Sein Werk hat weit über die Zeit, in der es entstand, hinaus gewirkt, und die Methoden, die es anwandte, sind auch heute noch von zentraler Bedeutung für das moderne Ingenieurwesen und die moderne Architektur. Monge zeigte, dass sich die Geometrie als Analyseinstrument und als Quelle für weltverändernde Neuerungen eignet.

Darstellende Geometrie – Zusammenfassung
Gaspard Monges Darstellende Geometrie war ein grundlegender Schritt zur Organisation des räumlichen Denkens. Sie verband die Präzision der Mathematik mit den praktischen Anforderungen der Architektur und des Ingenieurwesens. Die Art und Weise, wie Menschen Strukturen entwarfen und verstanden, änderte sich mit der Einführung rechtwinkliger Projektionen zur Darstellung der dreidimensionalen Realität auf einer zweidimensionalen Ebene.
Obwohl Monge in späteren Jahren kritisiert und zu komplexeren Entwürfen herausgefordert wurde, legte er den Grundstein für eine Entwicklung, die Monge in den folgenden Jahrhunderten weiterentwickelte und verfeinerte. Die Darstellende Geometrie wurde zu einem universellen Werkzeug, zu einer Entwurfssprache. Sie wird noch heute von Ingenieuren und Architekten gleichermaßen gelehrt. Dank Monge erhielt die Idee, Funktionalität und Ästhetik in der Raumgestaltung zu verbinden, eine neue Dimension. In jeder Arbeit, die räumliches Denken erfordert, wird sein Vermächtnis deutlich.