Vad är deskriptiv geometri?
Innehållsförteckning
Sedan tidernas begynnelse har mänskligheten sökt efter sätt att korrekt representera rum på ett begripligt och ordnat sätt. Även om enkla teckningar eller diagram har tjänat människan sedan antiken, var det inte förrän Gaspard Monge på 1700-talet som dessa ansträngningar fick matematisk noggrannhet och universalitet. I grund och botten utgör deskriptiv geometri vetenskapen om att projicera rumsliga objekt på tvådimensionella plan på ett exakt och otvetydigt sätt.
Vad är grunden för deskriptiv geometri?
Den centrala idén med deskriptiv geometri är att projektioner på plan kan representera komplexa tredimensionella kroppar. Detta gör det möjligt att analysera deras struktur och rumsliga relationer samtidigt som man håller sig inom området för tvådimensionella ritningar. Detta tillvägagångssätt är av stor betydelse inom teknik och arkitektur, där det ofta är avgörande att exakt planera strukturen hos en byggnad eller maskin innan man går vidare till genomförandet.
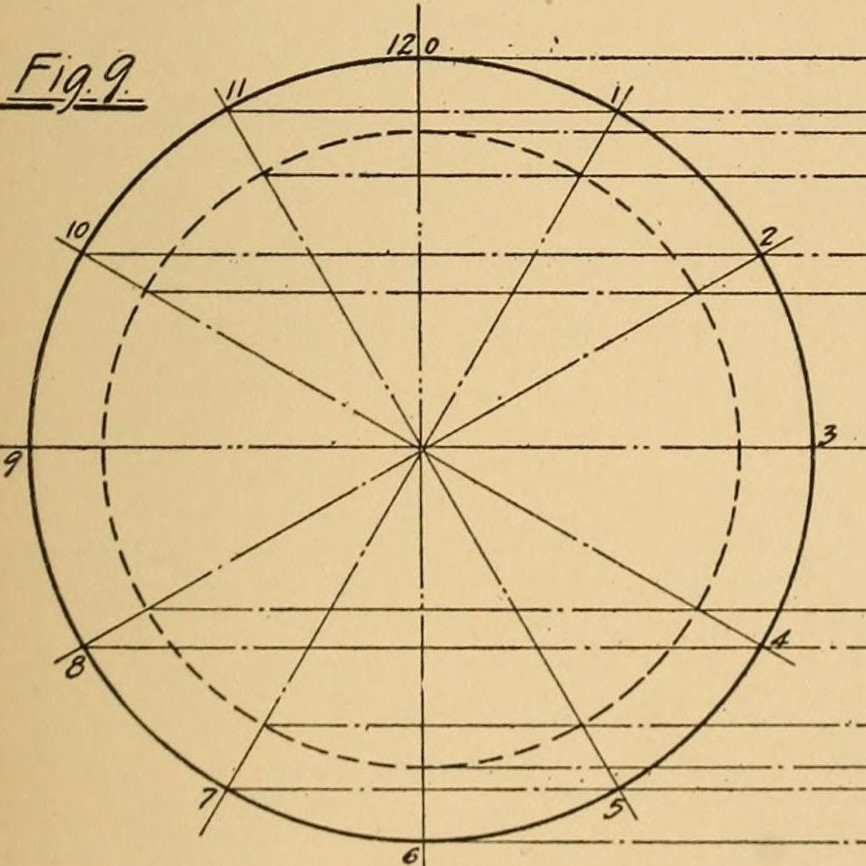
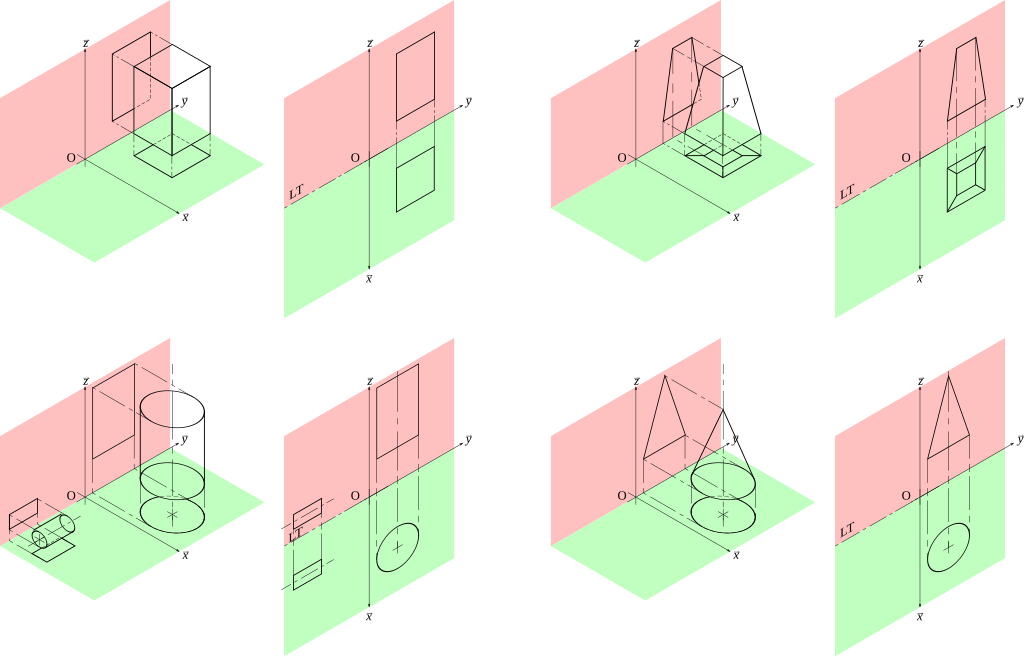
Beskrivande geometri ger ett enkelt sätt att förstå en rymd. Tack vare den rektangulära projektionen – en av de grundläggande teknikerna inom detta område – är det möjligt att se på en kropp från olika perspektiv, vilket gör denna metod till ett extremt mångsidigt verktyg. En bild sedd uppifrån (horisontell projektion), från sidan (lateral projektion) eller framifrån (vertikal projektion) fångar mycket information om ett objekt som kan analyseras i ett designsammanhang.
Dess fördel är dess förmåga att kombinera teoretisk matematik med praktiska tillämpningar. Utformningen av byggnader, broar eller maskiner bygger på förmågan att förutsäga hur de olika elementen kommer att samverka i verkligheten. Tack vare Monges metoder kunde ingenjörer planera och lösa konstruktionsproblem redan innan arbetet påbörjades på byggarbetsplatsen.
Disciplinens uppkomst och utveckling
Även om den deskriptiva geometrin numera betraktas som en grundläggande gren av den tillämpade matematiken, har den sitt ursprung i praktiska behov. På 1700-talet, när Gaspard Monge inledde sin karriär som ung militäringenjör, stötte han på ett problem som krävde noggrann modellering av rymden i samband med utformningen av befästningar. Konstruktionsprinciperna för sådana strukturer krävde stor noggrannhet, och de måste ha bombsäkra väggar och valv.
Vid 18 års ålder hade Monge redan utvecklat grunderna i ett system som gjorde det möjligt att representera komplexa tredimensionella objekt i två dimensioner. Men på grund av den strategiska betydelsen av denna kunskap betraktades hans upptäckter som en militär hemlighet och gjordes inte tillgängliga för allmänheten på många år. Det var inte förrän 1794, efter den franska revolutionen, som Monge delade med sig av sin kunskap och införde ritningsgeometri i läroplanen vid École Normale och den nygrundade École Polytechnique.
Införandet av ritningsgeometri i undervisningen vid École Polytechnique 1795 var en banbrytande händelse. Förutom sina utmärkta matematiska färdigheter hade Monge en fallenhet för att kommunicera komplexa idéer på ett begripligt och inspirerande sätt. Redan under hans första föreläsningar väckte det nya området stort intresse bland studenterna och blev grunden för den tekniska vetenskapen.
Monge definierade ritgeometri som ett verktyg med två huvudmål: för det första att möjliggöra en exakt representation av tredimensionella objekt i två dimensioner och för det andra att dra slutsatser om formerna och relationerna mellan dessa objekt. Tack vare dessa principer fick det nya området teoretiska och praktiska dimensioner, vilket gjorde att det snabbt kunde spridas.

Grundläggande begrepp inom ritningsgeometri
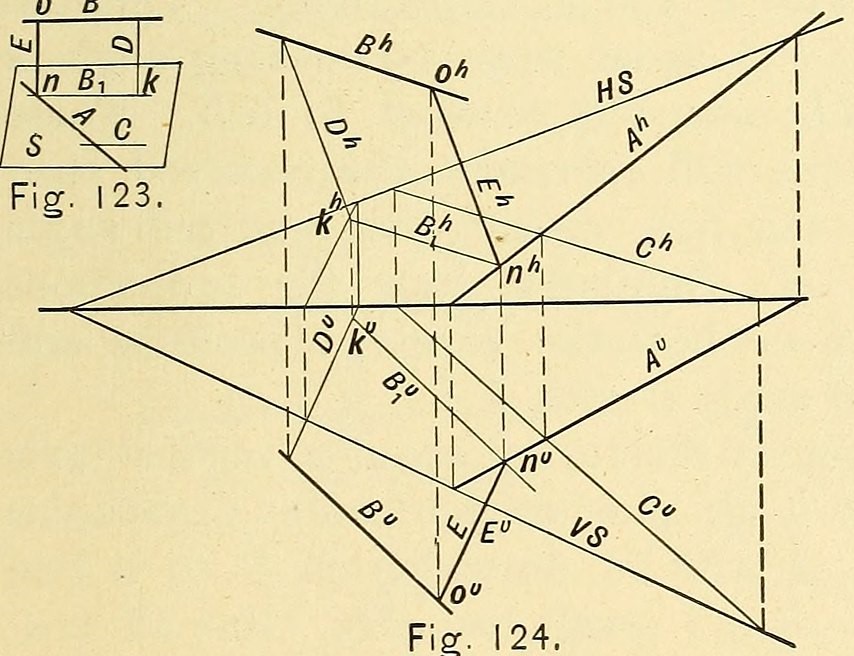
Det centrala elementet i ritningsgeometri är rektangulära projektioner, som gör att tredimensionella objekt kan representeras på en plan yta på ett otvetydigt sätt. Denna teknik gör det möjligt att skapa ritningar som återspeglar olika vyer av ett objekt: ovanifrån, framifrån och från sidan. Varje projektion visar olika aspekter av strukturen, vilket ger en fullständig förståelse för dess geometri.
Rektangulära projektioner, till exempel, visar hur praktiska de är vid byggnadsdesign. En byggnads planritning visar rummens utformning och placeringen av dörrar och fönster, medan vertikala projektioner visar fasadens höjd och proportioner. Med hjälp av sidoprojektioner kan man dessutom analysera djupet och detaljerna i konstruktionen, t.ex. takutsprång eller fasaddetaljer.
Ritningsgeometri gör det också möjligt att lösa komplexa rumsliga problem, såsom genomträngning av kroppar. Inom arkitekturen används exemplet för att illustrera välvda tak, vilket hjälper till att avgöra hur de olika elementen sitter ihop. Inom maskinteknik används dessa tekniker vid konstruktion av maskindelar, där varje komponent måste passa perfekt med de andra.
En av de viktigaste egenskaperna hos ritningsgeometri är dess mångsidighet. Med projektionsmetoden kan man skapa bilder av både enkla geometriska figurer och komplexa former, som exempelvis ellipsoid- eller hyperboloidytor. Gaspard Monge bidrog på ett ovärderligt sätt till att införa denna teknik i designpraxis och gjorde ritningsgeometrin till ett verktyg som kombinerar matematisk precision med estetik och funktionalitet.
Tack vare ritningsgeometrin blev det också möjligt att visualisera koncept som tidigare legat inom fantasins sfär. Dessa tekniker är inte bara ett verktyg för att skapa ritningar utan också ett verktyg för rumslig analys för att förstå och optimera konstruktioner.
Monges tillämpningar och innovationer
En av Gaspard Monges mest imponerande prestationer var tillämpningen av principerna för ritningsgeometri för att lösa praktiska konstruktionsproblem. Hans forskning var inte begränsad till att skapa teoretiska rumsliga modeller utan omfattade även specifika ingenjörsmetoder, som stereotomi – vetenskapen om att skära sten, vars tillämpning på valv och murbruksfria konstruktioner revolutionerade 1700-talets arkitektur.
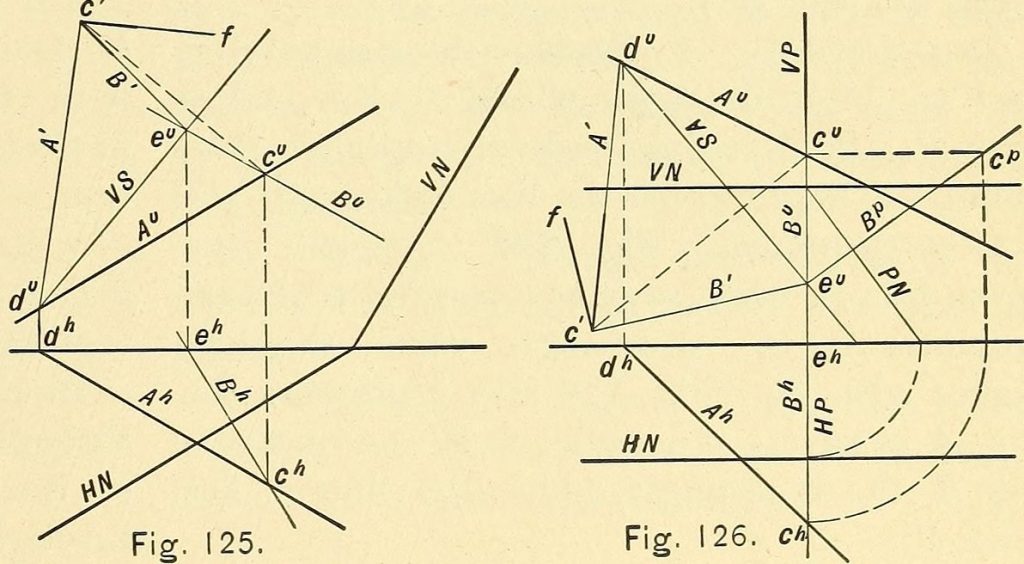
Monge konstaterade att en viktig del i framgångsrik design är att förstå kurvaturlinjerna på föremålens yta. Dessa linjer, ett ortogonalt arrangemang på ytan, ger en estetisk betoning på dess karaktär och, viktigast av allt, underlättar planeringen av uppdelningen av strukturella element. Dessa principer gjorde det möjligt att bygga stenvalv av exakt matchande element som bildade stabila strukturer utan att använda murbruk.
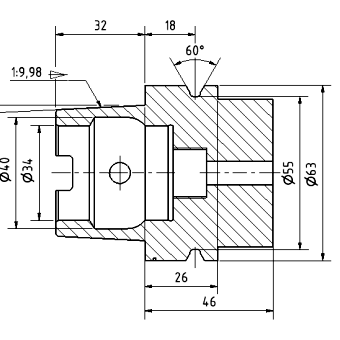
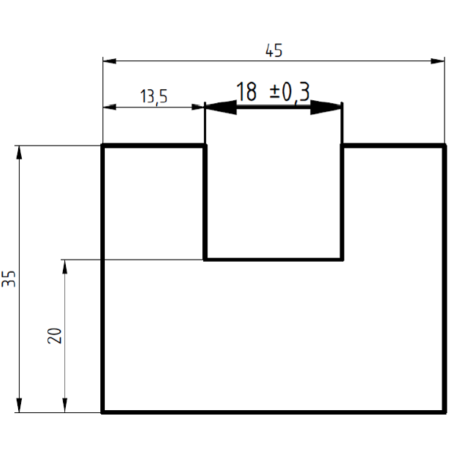
Monges innovation var inte begränsad till arkitektoniska strukturer. Hans metoder har också tillämpats inom maskinteknik, där noggrannhet i konstruktionen är avgörande. Rektangulär projektion användes vid maskinkonstruktion, vilket gjorde det möjligt att exakt definiera formerna och proportionerna på enskilda delar och hur de passar ihop.
Ett annat genombrott var kombinationen av ritningsgeometri och estetik. Monge ansåg att konstruktionslinjerna skulle återspegla karaktären hos den yta de befinner sig på. Därmed introducerade han en ny kvalitet i den arkitektoniska utformningen, där form och funktion kompletterar varandra. Skiljelinjer på valv eller husfasader blev ett dekorativt element som gav helheten ett harmoniskt utseende.
Monge visade att geometri inte bara är ett matematiskt verktyg utan ett universellt språk som kombinerar teoretiska grunder med de praktiska behoven inom konstruktion och design. Som ett resultat förblir hans prestationer relevanta och inspirerar efterföljande generationer av designers.
Kritik och inflytande av ritningsgeometri
Trots den revolutionerande karaktären hos ritningsgeometrin och dess mångsidiga tillämpningar var Gaspard Monges teori inte fri från begränsningar och mötte kritik, särskilt i samband med mer komplexa strukturer. Det första och mest framträdande problemet var svårigheten att tillämpa stereotomiprinciperna på konstruktioner med mer ovanliga former, som diagonala broar eller valv med icke-utvidgningsbara ytor.
Ett exempel på dessa begränsningar var broar som byggdes i Europa på 1800-talet, särskilt konstruktioner som utformades för tågpassage. När det gäller diagonala broar, där vinkeln mellan vägen och järnvägen var liten, gav Monges ritningsgeometri inte alltid tillräckliga verktyg för optimal kraftfördelning. Som kritikerna påpekade motsvarade de krökningslinjer, som Monge föreslog som ett viktigt konstruktionselement, inte alltid de faktiska mekaniska kraven, såsom tryckfördelning eller vibrationsmotstånd.
Även om kritiken är fullt berättigad förminskar den inte Monges betydelse som grundare av den grundläggande metodiken för rumslig geometri. Hans arbete inspirerade generationer av ingenjörer som utvecklade och anpassade hans metoder till nya tekniska utmaningar. Under andra halvan av 1800-talet utvecklades till exempel konstruktionstekniken i takt med att elasticitetsteorin och materialvetenskapen utvecklades, vilket gav en bättre förståelse för konstruktioners komplexa mekaniska beteende.
Monges inflytande var också tydligt i den senare utvecklingen av arkitektur och teknik under 1900-talet. I den moderna eran, introducerade strukturer som betongskal och lätta stålkonstruktioner helt nya designmöjligheter, men samtidigt baserades de på de grundläggande principerna för ritningsgeometri. Monges idéer, som kombinerade teori och praktik, låg till grund för utvecklingen av dessa innovativa tekniker.
Monge lämnade också efter sig ett bestående avtryck i den tekniska utbildningen. Hans synsätt, som betonar praktiska tillämpningar av geometri, har anammats av tekniska skolor över hela världen. Hans undervisningsmetoder, som bygger på en tydlig presentation av förhållandet mellan rumsliga kroppar och deras projektioner, har blivit grunden för utbildningen av ingenjörer och arkitekter.
Sammanfattningsvis kan sägas att den kritik som vissa aspekter av Monges teori mötte var en utgångspunkt för den fortsatta utvecklingen av ritningsgeometrin snarare än ett förnekande av den. Effekten av hans arbete sträcker sig långt bortom den tid han levde i, och hans metoder är fortfarande en viktig del av modern ingenjörskonst och arkitektur. Monge visade att geometriskt tänkande kan vara ett verktyg för analys och en källa till innovation som förändrar världen.

Deskriptiv geometri – sammanfattning
Gaspard Monges deskriptiva geometri var ett grundläggande steg mot att organisera rumsligt tänkande. Den kombinerade matematikens precision med de praktiska kraven inom arkitektur och ingenjörskonst. Införandet av rektangulära projektioner för att representera den tredimensionella verkligheten på ett tvådimensionellt plan förändrade hur människor konstruerade och förstod strukturer.
Trots senare kritik och utmaningar vid mer komplexa konstruktioner, lade Monge en grund som utvecklades och förfinades under de följande århundradena. Deskriptiv geometri blev ett universellt verktyg, ett designspråk som än i dag lärs ut till både ingenjörer och arkitekter. Idén om att kombinera funktionalitet med estetik i rumslig design fick en ny dimension tack vare Monge. Hans arv är fortfarande tydligt i alla arbeten som involverar rumsligt tänkande.