Mitä on kuvaileva geometria?
Sisällysluettelo
Ihmiskunta on aikojen alusta lähtien etsinyt keinoja kuvata avaruutta tarkasti, selkeästi ja järjestelmällisesti. Vaikka yksinkertaiset piirrokset tai kaaviot ovat palvelleet ihmisiä antiikin ajoista lähtien, vasta Gaspard Mongen työ 1700-luvulla toi näihin pyrkimyksiin matemaattisen tarkkuuden ja yleispätevyyden. Kuvaileva geometria on pohjimmiltaan tiede, jossa avaruudellisia kohteita projisoidaan kaksiulotteisille tasoille täsmällisesti ja yksiselitteisesti.
Mihin kuvaileva geometria perustuu?
Kuvailevan geometrian ydinajatus perustuu siihen, että kaksiulotteisilla projektioilla voidaan esittää monimutkaisia kolmiulotteisia aineita. Tämä mahdollistaa niiden rakenteen ja tilasuhteiden analysoinnin pysyen kuitenkin kaksiulotteisten piirrosten alueella. Tällä menetelmällä on suuri merkitys insinööritieteissä ja arkkitehtuurissa, joissa on usein ratkaisevan tärkeää suunnitella tarkasti rakennuksen tai koneen rakenne ennen sen toteuttamista.
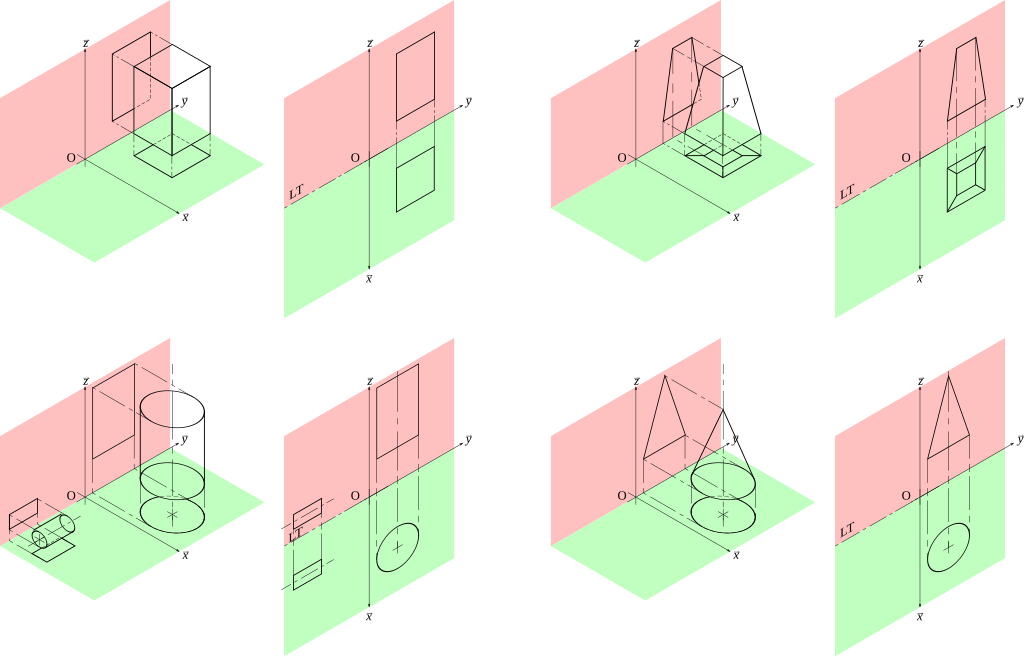
Kuvaileva geometria tarjoaa helpon tavan ymmärtää tilaa. Suorakulmaisten projektioiden, yhden keskeisimmistä tekniikoista, ansiosta on mahdollista tarkastella kiinteää ainetta eri näkökulmista, mikä tekee tästä menetelmästä erittäin monipuolisen työkalun. Ylhäältä (vaakaprojektio), sivulta (sivuprojektio) tai edestä (pystysuora projektio) katsottuna kuva tallentaa paljon tietoa kohteesta, jota voidaan analysoida suunnittelun yhteydessä.
Sen etuna on sen kyky yhdistää teoreettinen matematiikka ja käytännön sovellukset. Rakennusten, siltojen tai koneiden suunnittelu perustuu kykyyn ennustaa , miten eri elementit ovat vuorovaikutuksessa todellisuudessa. Mongen menetelmien ansiosta insinöörit pystyivät suunnittelemaan ja ratkaisemaan rakennusongelmia jo ennen kuin työmaalla edes aloitettiin.
Tieteenalan synty ja kehitys
Vaikka kuvailevaa geometriaa pidetään nykyään sovelletun matematiikan keskeisenä osa-alueena, se sai alkunsa käytännön tarpeista. Kun Gaspard Monge 1700-luvulla aloitti uransa nuorena sotilasinsinöörinä, hän kohtasi ongelman, joka vaati tiukkaa tilan mallintamista linnoitusten suunnittelun yhteydessä. Tällaisten rakenteiden rakennusperiaatteet edellyttivät suurta tarkkuutta, ja niissä oli oltava pomminkestävät seinät ja holvit.
Monge oli jo 18-vuotiaana kehittänyt perusteet järjestelmälle, jonka avulla monimutkaiset kolmiulotteiset kohteet voitiin esittää kaksiulotteisesti. Tämän tiedon strategisen merkityksen vuoksi hänen keksintöjään pidettiin kuitenkin sotilassalaisuutena, eikä niitä annettu yleisön saataville moneen vuoteen. Vasta vuonna 1794, Ranskan vallankumouksen jälkeen, Monge jakoi tietämyksensä ja otti käyttöön tyhjentävän geometrian École Normalen ja vastaperustetun École Polytechniquen opetussuunnitelmassa.
Piirrosgeometrian käyttöönotto École Polytechniquen opetuksessa vuonna 1795 oli käänteentekevä tapahtuma. Erinomaisten matemaattisten taitojensa lisäksi Mongella oli lahja välittää monimutkaisia ajatuksia ymmärrettävällä ja innostavalla tavalla. Jo hänen ensimmäisten luentojensa aikana uusi ala herätti suurta kiinnostusta opiskelijoiden keskuudessa ja siitä tuli teknisen tieteen perusta.
Monge määritteli kuvailevan geometrian välineeksi, jolla on kaksi päätavoitetta: mahdollistaa kolmiulotteisten kohteiden tarkka esittäminen kahdessa ulottuvuudessa ja tehdä päätelmiä näiden kohteiden muodoista ja keskinäisistä suhteista. Näiden periaatteiden ansiosta kuvaileva geometria levisi nopeasti ja sai sekä teoreettisia että käytännöllisiä ulottuvuuksia.

Luonnosgeometrian peruskäsitteet
Piirustusgeometrian keskeinen elementti on suorakulmaiset projektiot, joiden avulla kolmiulotteiset kohteet voidaan esittää tasaisella pinnalla yksiselitteisesti. Tämän tekniikan avulla voidaan luoda piirustuksia, jotka kuvaavat eri näkymiä esineestä: ylhäältä, edestä ja sivulta. Näiden näkymien avulla voidaan ymmärtää rakenteen geometriaa täydellisesti.
Esimerkiksi suorakulmaiset projektiot osoittavat niiden käytännöllisyyden rakennussuunnittelussa. Rakennuksen pohjapiirroksesta nähdään huoneiden sijoittelu sekä ovien ja ikkunoiden sijoittelu, kun taas pystysuuntaisista projektioista nähdään julkisivun korkeus ja mittasuhteet. Sivuprojektiot taas paljastavat rakenteen syvyyden ja yksityiskohtien, kuten katon ulkonemien tai julkisivun yksityiskohtien, analysoinnin.
Piirustusgeometria mahdollistaa myös monimutkaisten tilallisten ongelmien ratkaisemisen, kuten kiinteiden kappaleiden keskinäisen läpileikkauksen. Arkkitehtuurissa esimerkkiä käytetään havainnollistamaan holvikattoja, mikä auttaa määrittämään, miten eri elementit liittyvät toisiinsa. Konetekniikassa näitä tekniikoita käytetään koneen osien suunnittelussa, jossa jokaisen osan on sovittava täydellisesti toisiinsa.
Luonnosgeometrian keskeinen ominaisuus on sen monipuolisuus. Projektiomenetelmän avulla voidaan luoda kuvia sekä yksinkertaisista geometrisista kuvioista että monimutkaisista muodoista, kuten ellipsoidisista tai hyperboloidisista pinnoista. Tämän tekniikan käyttöönotto suunnittelukäytännössä oli Gaspard Mongen korvaamaton panos, sillä hän teki luonnosgeometriasta työkalun, jossa yhdistyvät matemaattinen tarkkuus, estetiikka ja toiminnallisuus.
Luonnosgeometrian ansiosta tuli myös mahdolliseksi visualisoida käsitteitä, jotka olivat aiemmin jääneet mielikuvituksen piiriin. Nämä tekniikat eivät ole vain työkalu piirustusten luomiseen vaan myös työkalu tila-analyysiin, jonka avulla voidaan ymmärtää ja optimoida malleja.
Mongen sovellukset ja innovaatiot
Gaspard Monge mullisti rakennussuunnittelun soveltamalla piirustusgeometrian periaatteiden soveltaminen käytännön rakennusongelmien ratkaisemiseen. Hänen tutkimuksensa ei rajoittunut teoreettisten tilamallien luomiseen, vaan sisälsi myös erityisiä insinöörimenetelmiä, kuten stereotomian eli kiven tarkkaan leikkaamiseen perustuvan tieteen, jonka soveltaminen holvimuuraukseen ja laastittomaan rakentamiseen toi 1700-luvun arkkitehtuuriin ennennäkemätöntä tarkkuutta ja kestävyyttä.
Monge huomautti, että onnistuneen suunnittelun avaintekijä on esineiden pinnalla olevien kaarevuuslinjojen oikea ymmärtäminen. Nämä pinnan ortogonaaliset linjat eivät ainoastaan korosta esteettisesti rakenteen luonnetta, vaan myös mahdollistavat tarkkuuden rakenneosien suunnittelussa ja leikkaamisessa. Näiden periaatteiden ansiosta kiviholvit voitiin koota tarkkaan sovitetuista elementeistä, jotka muodostivat vakaita rakenteita ilman laastin käyttöä.
Mongen innovaatio ei rajoittunut arkkitehtonisiin rakenteisiin. Hänen menetelmiään on sovellettu myös koneenrakennuksessa, jossa suunnittelun tarkkuus on ratkaisevan tärkeää. Koneiden suunnittelussa käytettiin suorakulmaista projektiota, jonka avulla voitiin määritellä tarkasti yksittäisten osien muodot ja mittasuhteet sekä se, miten ne sopivat yhteen.
Toinen läpimurto oli luonnosgeometrian ja estetiikan yhdistäminen. Monge uskoi, että rakenneviivojen olisi heijastettava sen pinnan luonnetta, jolla ne sijaitsevat. Tällä hän toi arkkitehtoniseen suunnitteluun uudenlaisen laadun, jossa muoto ja toiminnallisuus täydentävät toisiaan. Holvien tai rakennusten julkisivujen jakolinjoista tuli koristeellinen elementti, joka antaa kokonaisuudelle harmonisen ilmeen.
Monge osoitti, että piirustusgeometria on enemmän kuin pelkkä matemaattinen työkalu, se on universaali kieli, jossa teoreettiset perusteet yhdistyvät rakentamisen ja suunnittelun käytännön tarpeisiin. Tämän ansiosta hänen saavutuksensa ovat edelleen ajankohtaisia ja inspiroivat suunnittelijoiden toisia sukupolvia.
Piirustusgeometrian kritiikki ja vaikutusvalta
Vaikka luonnosgeometria oli vallankumouksellinen ja laajalti sovellettava, Mongen teoria ei ollut ilman rajoituksia, ja se kohtasi kritiikkiä. Erityisesti monimutkaisempien rakenteiden yhteydessä. Ensimmäinen ja merkittävin ongelma oli vaikeus soveltaa stereotomian periaatteita epätavallisemman muotoisiin rakenteisiin, kuten vinosiltoihin tai holveihin, joiden pinnat eivät ole laajenevia.
Esimerkkinä näistä rajoituksista olivat Euroopassa 1800-luvulla rakennetut sillat, erityisesti junien kulkua varten suunnitellut rakenteet. Viistosiltojen tapauksessa, joissa tien ja rautatien välinen kulma oli pieni, Mongen luonnosgeometria ei aina tarjonnut riittäviä välineitä voiman optimaaliseen jakautumiseen. Kuten kriitikot huomauttivat, Mongen keskeiseksi suunnitteluelementiksi ehdottamat kaarevuuslinjat eivät aina vastanneet todellisia mekaanisia vaatimuksia, kuten paineen jakautumista tai tärinänkestävyyttä.
Vaikka kritiikki on täysin perusteltua, se ei vähennä Mongen merkitystä avaruusgeometrian perusmenetelmien perustajana. Hänen työnsä innoitti insinöörisukupolvia, jotka kehittivät ja mukauttivat hänen menetelmiään uusiin teknisiin haasteisiin. Esimerkiksi 1800-luvun jälkipuoliskolla suunnittelutekniikat kehittyivät kimmoteorian ja materiaalitieteen kehittymisen myötä, mikä mahdollisti rakenteiden monimutkaisen mekaanisen käyttäytymisen paremman ymmärtämisen.
Mongen vaikutus näkyi myös arkkitehtuurin ja tekniikan myöhemmässä kehityksessä 1900-luvulla. Nykyaikana rakenteet, kuten betonikuoret ja kevyet teräsrakenteet, toivat mukanaan aivan uusia suunnittelumahdollisuuksia, mutta samalla ne perustuivat luonnosgeometrian perusperiaatteisiin. Mongen teoriaa ja käytäntöä yhdistävät ajatukset olivat perusta näiden innovatiivisten tekniikoiden kehittämiselle.
Monge jätti pysyvän jäljen myös tekniseen koulutukseen. Hänen geometrian käytännön sovelluksia korostava lähestymistapansa on otettu käyttöön teknisissä oppilaitoksissa kaikkialla maailmassa. Hänen opetusmenetelmistään, jotka perustuvat avaruudellisten kappaleiden ja niiden projektioiden välisen suhteen selkeään esittämiseen, on tullut insinöörien ja arkkitehtien koulutuksen perusta.
Yhteenvetona voidaan todeta, että Mongen teorian joihinkin näkökohtiin kohdistunut kritiikki oli pikemminkin lähtökohta piirustusgeometrian jatkokehitykselle kuin sen kieltämiselle. Mongen työn vaikutus ulottuu kauas hänen aikakautensa ulkopuolelle, ja hänen menetelmänsä ovat edelleen keskeinen osa nykyaikaista insinöörityötä ja arkkitehtuuria. Monge osoitti, että geometrinen ajattelu voi olla analyysin väline ja maailmaa muuttavien innovaatioiden lähde.

Kuvaileva geometria – Yhteenveto
Gaspard Mongen kuvaileva geometria oli perustavanlaatuinen askel kohti avaruudellisen ajattelun järjestämistä. Se yhdisti matematiikan tarkkuuden arkkitehtuurin ja insinööritieteiden käytännön vaatimuksiin. Suorakulmaisten projektioiden käyttöönotto kolmiulotteisen todellisuuden esittämiseksi kaksiulotteisella tasolla muutti ihmisten tapaa suunnitella ja ymmärtää rakenteita.
Vaikka Monge kohtasi kritiikkiä erityisesti monimutkaisempien mallien osalta, hänen työnsä loi vankan perustan, jota seuraavat sukupolvet kehittivät ja hienosäätivät vastaamaan yhä vaativampia teknisiä haasteita. Kuvailevasta geometriasta tuli yleismaailmallinen työkalu, suunnittelukieli , jota insinöörit ja arkkitehdit opettavat vielä tänäkin päivänä. Ajatus toiminnallisuuden ja estetiikan yhdistämisestä tilasuunnittelussa sai uuden ulottuvuuden Mongen ansiosta. Hänen perintönsä on edelleen ilmeinen kaikissa töissä, joihin liittyy avaruudellinen ajattelu.