¿Qué es la geometría descriptiva?
Índice
Desde el principio de los tiempos, la humanidad ha buscado la manera de representar con precisión el espacio de forma comprensible y ordenada. Aunque los dibujos o diagramas sencillos han servido a los humanos desde la antigüedad, no fue hasta la obra de Gaspard Monge en el siglo XVIII cuando se dotó a estos esfuerzos de precisión matemática y universalidad. En esencia, la geometría descriptiva es la ciencia de proyectar objetos espaciales sobre planos bidimensionales de forma precisa y sin ambigüedades.
¿En qué se basa la geometría descriptiva?
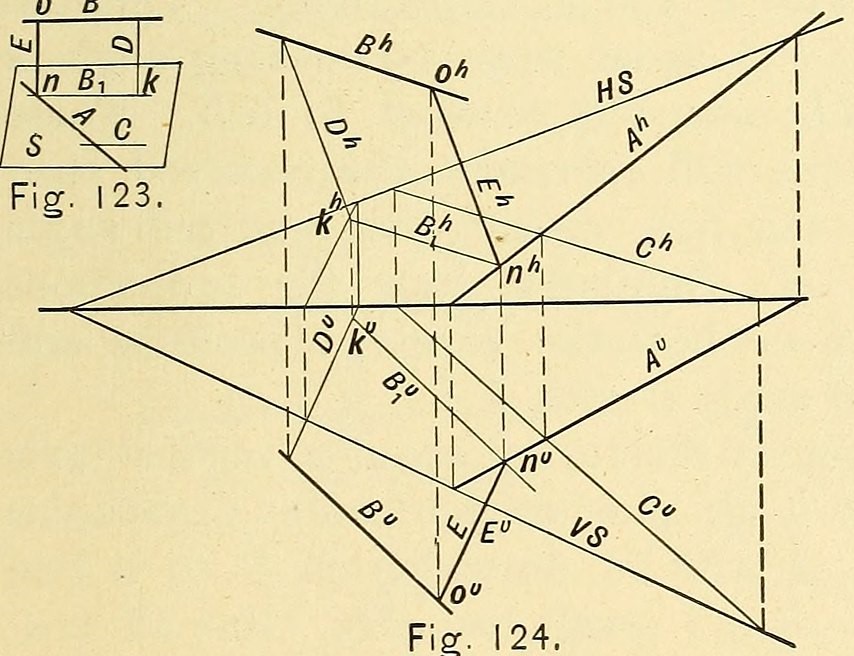
La idea central de la geometría descriptiva es que las proyecciones sobre planos pueden representar sólidos tridimensionales complejos. Esto permite analizar su estructura y sus relaciones espaciales sin salirse del ámbito de los dibujos bidimensionales. Este planteamiento es de gran importancia en ingeniería y arquitectura, donde a menudo es crucial planificar con precisión la estructura de un edificio o una máquina antes de proceder a su ejecución.
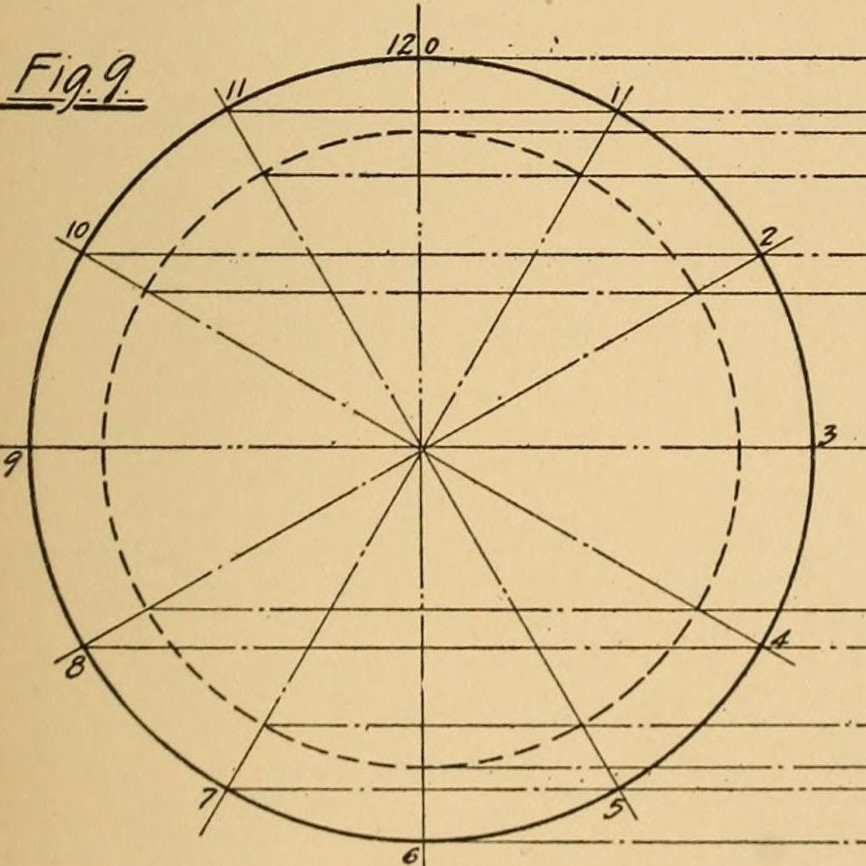
La geometría descriptiva facilita la comprensión del espacio. Gracias a la proyección rectangular, una de las técnicas básicas de este campo, es posible contemplar un sólido desde diferentes perspectivas, lo que convierte a este método en una herramienta extremadamente versátil. Una imagen vista desde arriba (proyección horizontal), desde un lado (proyección lateral) o desde delante (proyección vertical) capta mucha información sobre un objeto que puede analizarse en un contexto de diseño.
Su ventaja es la capacidad de combinar las matemáticas teóricas con las aplicaciones prácticas. El diseño de edificios, puentes o maquinaria se basa en la capacidad de predecir cómo interactuarán los distintos elementos en la realidad. Gracias a los métodos de Monge, los ingenieros pudieron planificar y resolver problemas de construcción antes incluso de que comenzaran los trabajos en la obra.
Génesis y desarrollo de la disciplina
Aunque actualmente se considera una rama fundamental de las matemáticas aplicadas, la geometría descriptiva debe sus orígenes a necesidades prácticas. En el siglo XVIII, cuando Gaspard Monge comenzó su carrera como joven ingeniero militar, se encontró con un problema que requería una modelización rigurosa del espacio en el contexto del diseño de fortificaciones. Los principios de construcción de tales estructuras exigían una gran precisión, y debían tener muros y bóvedas a prueba de bombas.
A los dieciocho años, Monge ya había desarrollado los fundamentos de un sistema que permitía representar objetos tridimensionales complejos en dos dimensiones. Sin embargo, debido a la importancia estratégica de estos conocimientos, sus descubrimientos se consideraron secreto militar y no se hicieron públicos durante muchos años. No fue hasta 1794, tras la Revolución Francesa, cuando Monge compartió sus conocimientos e introdujo la Geometría delineante en los planes de estudio de la École Normale y de la recién fundada École Polytechnique.
La introducción de la Geometría delineante en la enseñanza de la École Polytechnique en 1795 marcó un hito. Además de sus excelentes conocimientos matemáticos, Monge tenía el don de comunicar ideas complejas de forma comprensible e inspiradora. Ya durante sus primeras clases, el nuevo campo despertó gran interés entre los estudiantes y se convirtió en la base de la ciencia técnica.
Monge definió la geometría delineante como una herramienta con dos objetivos principales: en primer lugar, permitir la representación precisa de objetos tridimensionales en dos dimensiones; en segundo lugar, extraer conclusiones sobre las formas y las relaciones entre estos objetos. Gracias a estos principios, el nuevo campo adquirió dimensiones teóricas y prácticas, lo que permitió su rápida difusión.

Conceptos básicos de la geometría del dibujo
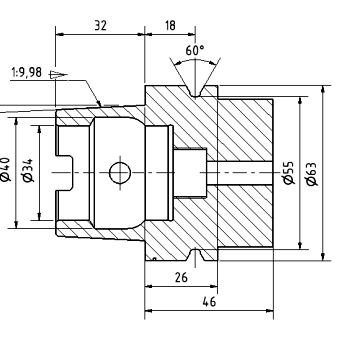
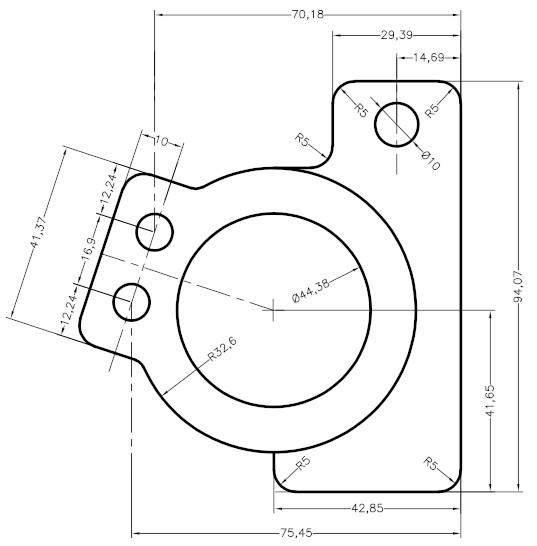
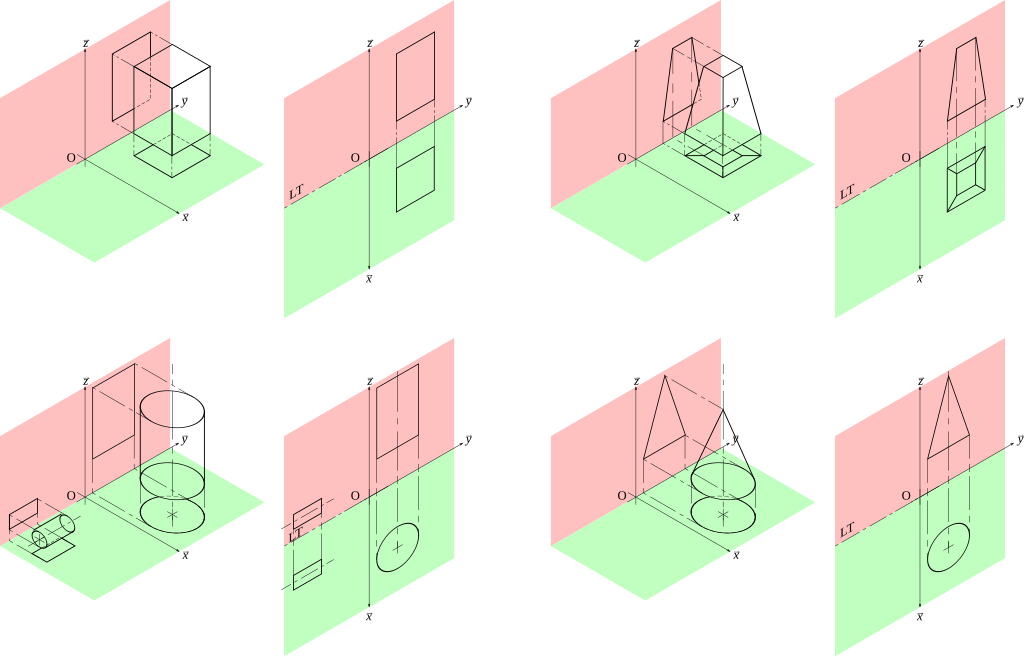
El elemento central de la geometría del dibujo son las proyecciones rectangulares, que permiten representar objetos tridimensionales sobre una superficie plana de forma inequívoca. Esta técnica permite crear dibujos que reflejan distintas vistas de un objeto: desde arriba, desde delante y desde un lado. Cada proyección muestra diversos aspectos de la estructura, lo que permite una comprensión completa de su geometría.
Las proyecciones rectangulares, por ejemplo, demuestran su utilidad en el diseño de edificios. La planta de un edificio muestra la distribución de las habitaciones y la disposición de puertas y ventanas, mientras que las proyecciones verticales muestran la altura y las proporciones de la fachada. Además, las proyecciones laterales permiten analizar la profundidad y los detalles de la estructura, como los salientes del tejado o los detalles de la fachada.
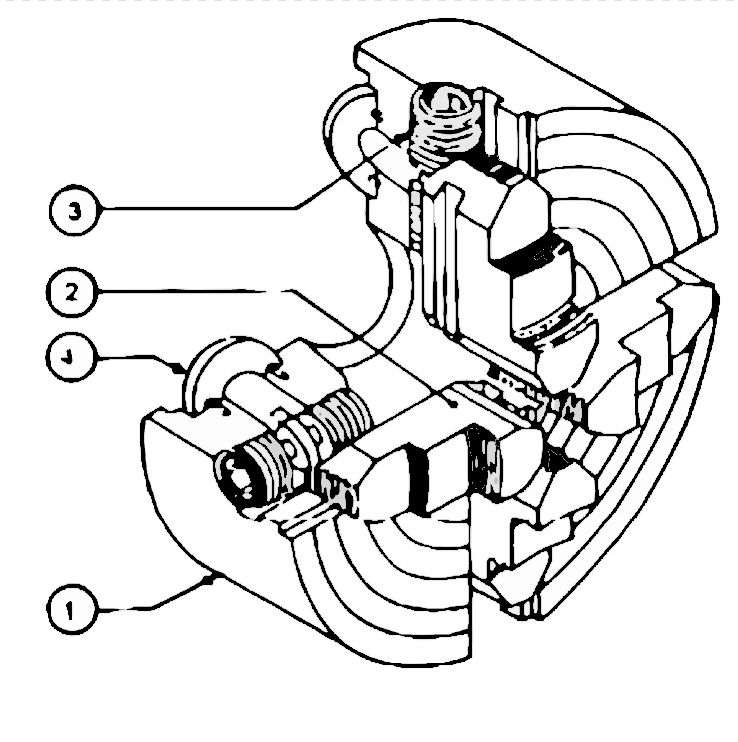
La geometría del dibujo también permite resolver problemas espaciales complejos, como la interpenetración de sólidos. En arquitectura, el ejemplo se utiliza para ilustrar cubiertas abovedadas, lo que ayuda a determinar cómo se unen los distintos elementos. En ingeniería mecánica, estas técnicas se utilizan en el diseño de piezas de máquinas, donde cada componente debe encajar perfectamente con los demás.
Una característica clave del dibujo geométrico es su versatilidad. El método de proyección permite crear imágenes tanto de figuras geométricas sencillas como de formas complejas, como superficies elipsoidales o hiperboloides. La introducción de esta técnica en la práctica del diseño fue la inestimable contribución de Gaspard Monge, que convirtió la geometría de trazado en una herramienta que combina la precisión matemática con la estética y la funcionalidad.
Gracias a la geometría de trazado, también fue posible visualizar conceptos que antes permanecían en el ámbito de la imaginación. Estas técnicas no son solo una herramienta para crear dibujos, sino también una herramienta de análisis espacial para comprender y optimizar los diseños.
Aplicaciones e innovaciones de Monge
Uno de los logros más impresionantes de Gaspard Monge fue la aplicación de los principios de la geometría del dibujo a la solución de problemas prácticos de construcción. Sus investigaciones no se limitaron a la creación de modelos espaciales teóricos, sino que también incluyeron métodos específicos de ingeniería, como la estereotomía y la ciencia del corte de la piedra, cuya aplicación a las bóvedas y a la construcción sin argamasa revolucionó la arquitectura del siglo XVIII.
Monge señaló que un elemento clave para el éxito del diseño es la comprensión adecuada de las líneas de curvatura de la superficie de los objetos. Estas líneas, una disposición ortogonal en la superficie, proporcionan un énfasis estético a su carácter y, lo que es más importante, facilitan la planificación de la división de los elementos estructurales. Estos principios permitieron ensamblar bóvedas de piedra a partir de elementos exactamente emparejados que formaban estructuras estables sin utilizar mortero.
La innovación de Monge no se limitó a las estructuras arquitectónicas. Sus métodos también se han aplicado en ingeniería mecánica, donde la precisión del diseño es crucial. La proyección rectangular se utilizó en el diseño de máquinas, lo que permitió definir con precisión las formas y proporciones de las piezas individuales y cómo encajan entre sí.
Otro avance fue la combinación de la geometría de trazado y la estética. Monge creía que las líneas de construcción debían reflejar el carácter de la superficie en la que se encontraban. Con ello, introdujo una nueva cualidad en el diseño arquitectónico, en la que forma y funcionalidad se complementan. Las líneas divisorias de las bóvedas o las fachadas de los edificios se convirtieron en un elemento decorativo que daba un aspecto armonioso al conjunto.
Monge demostró que la geometría del delineante no es solo una herramienta matemática, sino un lenguaje universal que combina los fundamentos teóricos con las necesidades prácticas de la construcción y el diseño. Como resultado, sus logros siguen siendo relevantes e inspiran a sucesivas generaciones de diseñadores.
Críticas e influencia de la geometría de trazado
A pesar de la naturaleza revolucionaria de la geometría de trazado y sus versátiles aplicaciones, la teoría de Gaspard Monge no estuvo exenta de limitaciones y se enfrentó a críticas, especialmente en el contexto de estructuras más complejas. El primer problema, y el más destacado, era la dificultad de aplicar los principios de la estereotomía a estructuras con formas más inusuales, como puentes diagonales o bóvedas con superficies no dilatables.
Un ejemplo de estas limitaciones fueron los puentes construidos en Europa en el siglo XIX, en particular las estructuras diseñadas para el paso de trenes. En el caso de los puentes diagonales, en los que el ángulo entre la carretera y el ferrocarril era escaso, la geometría de trazado de Monge no siempre proporcionaba las herramientas adecuadas para conseguir una distribución óptima de las fuerzas. Como señalaban los críticos, las líneas de curvatura que Monge proponía como elemento clave del diseño no siempre se correspondían con los requisitos mecánicos reales, como la distribución de la presión o la resistencia a las vibraciones.
Aunque plenamente justificadas, estas críticas no restan importancia a Monge como fundador de la metodología básica de la geometría espacial. Su obra inspiró a generaciones de ingenieros que desarrollaron y adaptaron sus métodos a los nuevos retos técnicos. En la segunda mitad del siglo XIX, por ejemplo, las técnicas de diseño evolucionaron con el desarrollo de la teoría de la elasticidad y la ciencia de los materiales, que permitieron comprender mejor el complejo comportamiento mecánico de las estructuras.
La influencia de Monge también fue evidente en el desarrollo posterior de la arquitectura y la ingeniería en el siglo XX. En la era moderna, estructuras como las cubiertas de hormigón y las estructuras ligeras de acero introdujeron posibilidades de diseño totalmente nuevas, pero al mismo tiempo se basaban en los principios básicos de la geometría de trazado. Las ideas de Monge, que combinaban teoría y práctica, fueron la base del desarrollo de estas tecnologías innovadoras.
Monge también dejó una huella imborrable en la enseñanza técnica. Su enfoque, que hace hincapié en las aplicaciones prácticas de la geometría, se ha adoptado en escuelas técnicas de todo el mundo. Sus métodos de enseñanza, basados en una presentación clara de la relación entre los sólidos espaciales y sus proyecciones, se han convertido en la base de la educación de ingenieros y arquitectos.
En resumen, las críticas a las que se enfrentaron algunos aspectos de la teoría de Monge fueron un punto de partida para el desarrollo ulterior de la geometría de trazado y no su negación. El impacto de su obra se extiende mucho más allá de la época en que vivió, y sus métodos siguen siendo un elemento clave de la ingeniería y la arquitectura modernas. Monge demostró que el pensamiento geométrico puede ser una herramienta de análisis y una fuente de innovación que cambie el mundo.

Geometría descriptiva – Resumen
La geometría descriptiva de Gaspard Monge fue un paso fundamental hacia la organización del pensamiento espacial, ya que combinaba la precisión de las matemáticas con los requisitos prácticos de la arquitectura y la ingeniería. La introducción de proyecciones rectangulares para representar la realidad tridimensional en un plano bidimensional cambió la forma de diseñar y entender las estructuras.
A pesar de las críticas posteriores y los desafíos a diseños más complejos, Monge sentó unas bases desarrolladas y perfeccionadas a lo largo de los siglos siguientes. La geometría descriptiva se convirtió en una herramienta universal, un lenguaje de diseño que siguen enseñando ingenieros y arquitectos. La idea de combinar funcionalidad y estética en el diseño espacial adquirió una nueva dimensión gracias a Monge. Su legado sigue siendo evidente en cualquier obra que implique pensamiento espacial.