Czym jest geometria wykreślna?
Spis treści
Od zarania dziejów ludzkość poszukiwała sposobów na dokładne przedstawienie przestrzeni w sposób zrozumiały i uporządkowany. Choć proste rysunki czy schematy służyły ludziom od starożytności, to dopiero prace Gasparda Monge’a w XVIII wieku nadały tym wysiłkom matematyczną ścisłość i uniwersalność. Geometria wykreślna, w swojej istocie, jest nauką o rzutowaniu przestrzennych obiektów na dwuwymiarowe płaszczyzny w sposób precyzyjny i jednoznaczny.
Na czym polega geometria wykreślna?
Centralnym założeniem geometrii wykreślnej jest możliwość przedstawienia złożonych brył trójwymiarowych za pomocą rzutów na płaszczyzny. Dzięki temu można analizować ich strukturę i relacje przestrzenne, pozostając w sferze dwuwymiarowych rysunków. Takie podejście ma ogromne znaczenie w inżynierii i architekturze, gdzie niejednokrotnie kluczowe jest precyzyjne zaplanowanie struktury budynku czy maszyny, zanim przejdzie się do ich realizacji.
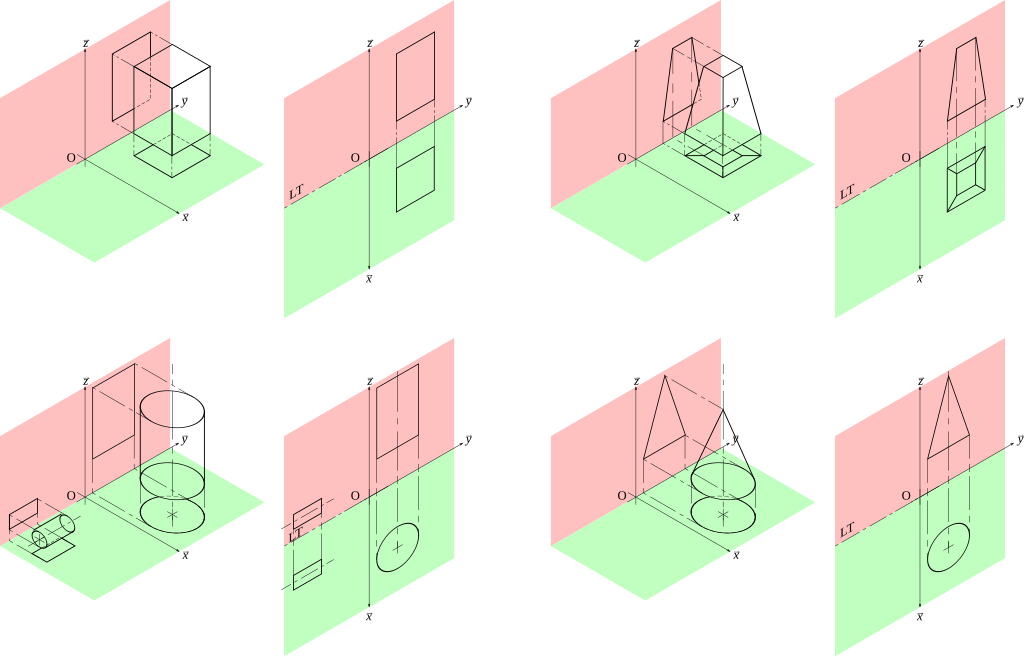
Geometria wykreślna pozwala w łatwy sposób zrozumieć przestrzeń. Dzięki rzutowi prostokątnemu – jednej z podstawowych technik tej dziedziny – możliwe jest spojrzenie na bryłę z różnych perspektyw, co czyni tę metodę niezwykle uniwersalnym narzędziem. Obraz widziany z góry (rzut poziomy), z boku (rzut boczny) czy z przodu (rzut pionowy) oddaje dużo informacji o obiekcie, które można analizować w kontekście projektowym.
Jej zaletą jest zdolność do łączenia teoretycznej matematyki z praktycznymi zastosowaniami. Projektowanie budynków, mostów czy maszyn opiera się na zdolności przewidywania, jak poszczególne elementy będą ze sobą współgrały w rzeczywistości. Dzięki metodom Monge’a inżynierowie mogli nie tylko planować, ale także rozwiązywać problemy konstrukcyjne, zanim w ogóle rozpoczęto pracę na placu budowy.
Geneza i rozwój dyscypliny
Geometria wykreślna, choć obecnie uznawana za fundamentalną dziedzinę matematyki stosowanej, swoje początki zawdzięcza potrzebom praktycznym. W XVIII wieku, gdy Gaspard Monge rozpoczął swoją karierę jako młody inżynier wojskowy, napotkał na problem wymagający ścisłego modelowania przestrzeni w kontekście projektowania fortyfikacji. Zasady konstrukcji takich struktur wymagały ogromnej dokładności, musiały posiadać one odporne na bombardowania mury i sklepienia.
Już w wieku 18 lat Monge opracował podstawy systemu, który pozwalał na przedstawianie złożonych obiektów trójwymiarowych w dwóch wymiarach. Jednak ze względu na strategiczne znaczenie tej wiedzy, jego odkrycia zostały uznane za tajemnicę wojskową i przez wiele lat nie były udostępniane publicznie. Dopiero w 1794 roku, po rewolucji francuskiej, Monge podzielił się swoją wiedzą, wprowadzając geometrię wykreślną do programu nauczania w École Normale oraz nowo założonej École Polytechnique.
Wprowadzenie geometrii wykreślnej do nauczania w École Polytechnique w 1795 roku było wydarzeniem przełomowym. Monge, oprócz doskonałych umiejętności matematycznych, posiadał dar przekazywania skomplikowanych idei w sposób zrozumiały i inspirujący. Już podczas pierwszych wykładów nowa dziedzina wzbudziła ogromne zainteresowanie wśród studentów i stała się podstawą nauk technicznych.
Monge definiował geometrię wykreślną jako narzędzie mające dwa główne cele: po pierwsze, umożliwienie precyzyjnego przedstawiania obiektów trójwymiarowych w dwóch wymiarach; po drugie, wyciąganie wniosków na temat kształtów i relacji między tymi obiektami. Dzięki tym zasadom nowa dziedzina zyskała zarówno wymiar teoretyczny, jak i praktyczny, co pozwoliło jej szybko się rozprzestrzenić.

Podstawowe koncepcje geometrii wykreślnej
Centralnym elementem geometrii wykreślnej są rzuty prostokątne, które umożliwiają przedstawienie trójwymiarowych obiektów na płaskiej powierzchni w sposób jednoznaczny. Dzięki tej technice możliwe jest tworzenie rysunków, które odzwierciedlają różne widoki obiektu: z góry, z przodu oraz z boku. Każdy z tych rzutów ukazuje inne aspekty konstrukcji, pozwalając na pełne zrozumienie jej geometrii.
Na przykładzie rzutów prostokątnych można zauważyć ich praktyczność w projektowaniu budynków. Rzut poziomy budynku przedstawia układ pomieszczeń oraz rozmieszczenie drzwi i okien, podczas gdy rzuty pionowe pokazują wysokość i proporcje elewacji. Dodatkowo rzuty boczne pozwalają na analizę głębokości i szczegółów konstrukcji, takich jak występy dachowe czy detale fasady.
Geometria wykreślna umożliwia także rozwiązywanie złożonych problemów przestrzennych, takich jak wzajemne przenikanie brył. W architekturze przykład ten znajduje zastosowanie w ilustrowaniu sklepionych dachów, pomaga to określić, jak poszczególne elementy łączą się w całość. W inżynierii mechanicznej techniki te wykorzystywane są w projektowaniu części maszyn, gdzie każdy element musi idealnie współgrać z pozostałymi.
Kluczową cechą geometrii wykreślnej jest jej uniwersalność. Metoda rzutowania pozwala tworzyć obrazy zarówno prostych figur geometrycznych, jak i skomplikowanych kształtów, takich jak powierzchnie elipsoidalne czy hiperboloidalne. Wprowadzenie tej techniki do praktyki projektowej było nieocenionym wkładem Gasparda Monge’a, który uczynił z geometrii wykreślnej narzędzie łączące precyzję matematyczną z estetyką i funkcjonalnością.
Dzięki geometrii wykreślnej możliwe stało się również wizualizowanie koncepcji, które wcześniej pozostawały w sferze wyobraźni. Techniki te są nie tylko narzędziem do tworzenia rysunków, ale także narzędziem do analizy przestrzennej, umożliwiającym zrozumienie i optymalizację projektów.
Zastosowania i innowacje Monge’a
Jednym z najbardziej imponujących osiągnięć Gasparda Monge’a było zastosowanie zasad geometrii wykreślnej do rozwiązywania praktycznych problemów konstrukcyjnych. Jego badania nie ograniczały się do tworzenia teoretycznych modeli przestrzennych, lecz obejmowały także konkretne metody inżynieryjne, takie jak stereotomia – nauka o cięciu kamienia, której zastosowanie w budowie sklepień i konstrukcji bez zaprawy zrewolucjonizowało architekturę XVIII wieku.
Monge zauważył, że kluczowym elementem skutecznego projektowania jest właściwe zrozumienie linii krzywizny na powierzchni obiektów. Linie te, będące ortogonalnym układem na powierzchni, stanowią nie tylko estetyczne podkreślenie jej charakteru, ale przede wszystkim ułatwiają planowanie podziału elementów konstrukcyjnych. Dzięki tym zasadom kamienne sklepienia mogły być składane z precyzyjnie dopasowanych elementów, które tworzyły stabilne konstrukcje bez użycia zaprawy.
Innowacyjność Monge’a nie ograniczała się do konstrukcji architektonicznych. Jego metody znalazły również zastosowanie w inżynierii mechanicznej, gdzie dokładność projektowania jest kluczowa. Przy projektowaniu maszyn stosowano rzutowanie prostokątne, które umożliwiało jednoznaczne określenie kształtów i proporcji poszczególnych części, a także ich wzajemnego dopasowania.
Kolejnym przełomem było połączenie geometrii wykreślnej z estetyką. Monge uważał, że linie konstrukcyjne powinny odzwierciedlać charakter powierzchni, na której się znajdują. Dzięki temu wprowadził nową jakość do projektowania architektonicznego, gdzie forma i funkcjonalność wzajemnie się uzupełniają. Linie podziału na sklepieniach czy fasadach budynków stały się elementem dekoracyjnym, nadającym harmonijny wygląd całości.
Monge pokazał, że geometria wykreślna nie jest jedynie narzędziem matematycznym, ale uniwersalnym językiem, który łączy teoretyczne podstawy z praktycznymi potrzebami budownictwa i projektowania. Dzięki temu jego osiągnięcia pozostają aktualne i inspirują kolejne pokolenia twórców.
Krytyka i wpływ geometrii wykreślnej
Pomimo rewolucyjnego charakteru geometrii wykreślnej i jej wszechstronnych zastosowań, teoria Gasparda Monge’a nie była wolna od ograniczeń i spotkała się z krytyką, zwłaszcza w kontekście bardziej skomplikowanych konstrukcji. Pierwszym i najbardziej widocznym problemem była trudność w zastosowaniu zasad stereotomii do struktur o bardziej nietypowych kształtach, takich jak mosty ukośne czy sklepienia o nierozwijalnych powierzchniach.
Jednym z przykładów tych ograniczeń były mosty budowane w XIX wieku w Europie, w szczególności obiekty przeznaczone do przejazdu pociągów. W przypadku mostów ukośnych, gdzie kąt między drogą a linią kolejową był niewielki, geometria wykreślna Monge’a nie zawsze dostarczała odpowiednich narzędzi do optymalnego rozkładu sił. Jak wskazywali krytycy, linie krzywizny, które Monge proponował jako kluczowy element projektowy, nie zawsze odpowiadały rzeczywistym wymaganiom mechanicznym, takim jak rozkład nacisków czy odporność na drgania.
Krytyka ta, choć w pełni uzasadniona, nie umniejsza znaczenia Monge’a jako twórcy podstawowej metodologii geometrii przestrzennej. Jego prace zainspirowały kolejne pokolenia inżynierów, którzy rozwijali jego metody, dostosowując je do nowych wyzwań technicznych. Na przykład w drugiej połowie XIX wieku techniki projektowe ewoluowały wraz z rozwojem teorii elastyczności i materiałoznawstwa, które pozwoliły na lepsze zrozumienie złożonych zachowań mechanicznych konstrukcji.
Wpływ Monge’a był widoczny także w późniejszym rozwoju architektury i inżynierii w XX wieku. W epoce nowoczesnej konstrukcje takie jak powłoki betonowe czy lekkie struktury stalowe wprowadziły zupełnie nowe możliwości projektowe, ale jednocześnie bazowały na podstawowych zasadach geometrii wykreślnej. Idee Monge’a, łączące teorię z praktyką, były fundamentem dla rozwoju tych nowatorskich technologii.
Monge pozostawił również trwały ślad w edukacji technicznej. Jego podejście, kładące nacisk na praktyczne zastosowania geometrii, zostało zaadaptowane w szkołach technicznych na całym świecie. Jego metody nauczania, oparte na jasnym przedstawianiu związków między bryłami przestrzennymi a ich rzutami, stały się podstawą kształcenia inżynierów i architektów.
Podsumowując, krytyka, z którą spotkały się niektóre aspekty teorii Monge’a, była raczej punktem wyjścia do dalszego rozwoju geometrii wykreślnej, niż jej zaprzeczeniem. Wpływ jego pracy wykracza daleko poza czasy, w których żył, a jego metody pozostają kluczowym elementem współczesnej inżynierii i architektury. Monge pokazał, że geometryczne myślenie może być nie tylko narzędziem analizy, ale także źródłem innowacji, które zmieniają świat.

Geometria wykreślna – Podsumowanie
Geometria wykreślna, rozwinięta przez Gasparda Monge’a, stanowiła fundamentalny krok w kierunku uporządkowania przestrzennego myślenia, które łączyło precyzję matematyki z wymaganiami praktycznymi architektury i inżynierii. Wprowadzenie rzutów prostokątnych jako narzędzia przedstawiającego trójwymiarową rzeczywistość na płaszczyźnie dwuwymiarowej, zmieniło sposób, w jaki ludzie projektowali i rozumieli konstrukcje.
Mimo późniejszej krytyki i wyzwań związanych z bardziej skomplikowanymi konstrukcjami, Monge stworzył podstawy, które przez kolejne wieki rozwijano i doskonalono. Geometria wykreślna stała się narzędziem uniwersalnym, językiem projektowania, który do dziś jest uczony zarówno przez inżynierów, jak i architektów. Dzięki Monge’owi idea łączenia funkcjonalności z estetyką w projektowaniu przestrzennym zyskała nowy wymiar. Jego dziedzictwo pozostaje widoczne w każdym dziele, które wymaga przestrzennego myślenia.