Géométrie descriptive
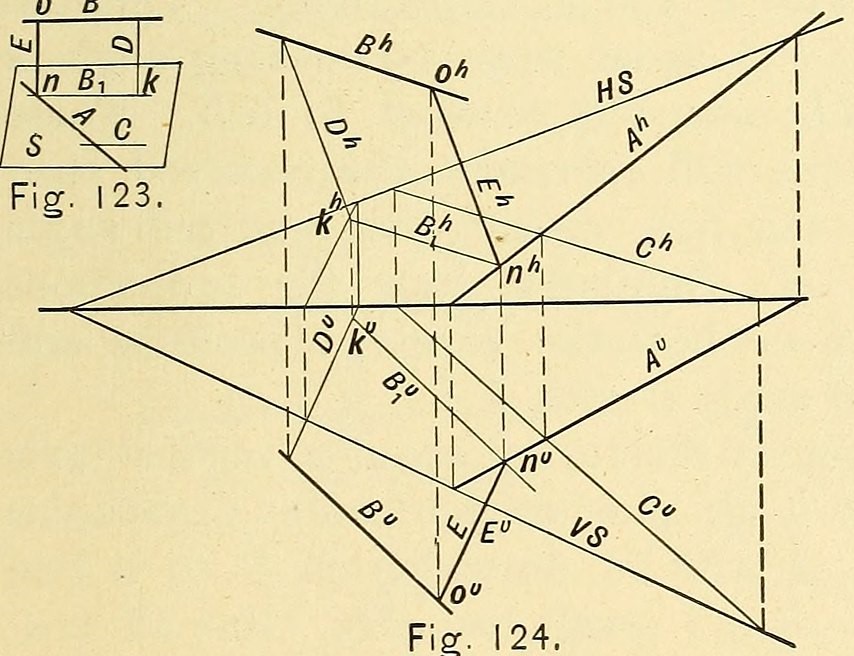
Table des matières
Depuis la nuit des temps, l’humanité a cherché des moyens de représenter l’espace avec précision, de manière compréhensible et ordonnée. Bien que de simples dessins ou diagrammes aient servi aux humains depuis l’Antiquité, ce n’est qu’au XVIIIe siècle, avec les travaux de Gaspard Monge, comte de Péluse, que ces efforts ont acquis une précision mathématique et une universalité. Fondamentalement, la géométrie descriptive est la science de la projection d’objets spatiaux sur des plans à deux dimensions de manière précise et non ambiguë.
Quelle est la base de la géométrie descriptive ?
L’idée centrale de la géométrie descriptive est que les projections sur des plans peuvent représenter des solides complexes en trois dimensions. Ceci permet d’analyser leur structure et leurs relations spatiales, tout en restant dans le domaine des dessins bidimensionnels. Cette approche revêt une grande importance en ingénierie et en architecture, où il est indispensable de planifier avec précision la structure d’un bâtiment ou d’une machine avant de procéder à sa mise en chantier.
La géométrie descriptive permet de comprendre facilement l’espace. Grâce à la projection rectangulaire, l’une des techniques de base de ce domaine, il est possible d’observer un solide sous différentes perspectives, ce qui fait de cette méthode un outil extrêmement polyvalent. Une image vue d’en haut (projection horizontale), de côté (projection latérale) ou de face (projection verticale) capture de nombreuses informations sur un objet qui peuvent être analysées dans un contexte de conception.
Son avantage réside dans sa capacité à combiner les mathématiques théoriques et les applications pratiques. La conception de bâtiments, de ponts ou de machines repose sur la capacité à prédire comment les différents éléments interagiront dans la réalité. Grâce aux méthodes de Monge, les ingénieurs ont donc pu planifier et résoudre les problèmes de construction avant même que les travaux ne commencent sur un chantier.
Genèse et développement de la discipline
Bien qu’elle soit aujourd’hui considérée comme une branche fondamentale des mathématiques appliquées, la géométrie descriptive doit ses origines à des besoins pratiques. Au XVIIIe siècle, lorsque Gaspard Monge entame sa carrière de jeune ingénieur militaire, il est confronté à un problème nécessitant une modélisation rigoureuse de l’espace dans le cadre de la conception de fortifications. Les principes de construction de ce type d’ouvrages exigent une grande précision et ils doivent avoir des murs et des voûtes à l’épreuve des projectiles.
À l’âge de 18 ans, Monge avait déjà développé les bases d’un système permettant de représenter en deux dimensions des objets complexes en trois dimensions. Toutefois, en raison de l’importance stratégique de telles connaissances, ses découvertes ont été considérées comme étant un secret militaire et n’ont pas été rendues publiques avant de nombreuses années. Ce n’est qu’en 1794, après la Révolution française, que Monge a partagé ses connaissances, introduisant la géométrie drainante dans le programme de l’École normale et de la nouvellement créée École polytechnique.
L’introduction de la géométrie du dessinateur, dans l’enseignement à polytechnique en 1795, fut un événement marquant. Outre ses excellentes compétences en mathématiques, Monge avait le don de communiquer des idées complexes d’une manière compréhensible et inspirante. Dès ses premiers cours, ce nouveau domaine suscite un grand intérêt parmi les étudiants et devient la base de la science technique.
Monge a défini la géométrie du dessinateur comme un outil ayant deux objectifs principaux. Premièrement, celui de permettre la représentation précise d’objets tridimensionnels en deux dimensions. Et deuxièmement, pouvoir tirer des conclusions sur les formes et les relations entre ces objets. Grâce à ces principes, le nouveau domaine a acquis des dimensions théoriques et pratiques, ce qui lui a permis de se répandre rapidement.

Concepts de base de la géométrie du dessin
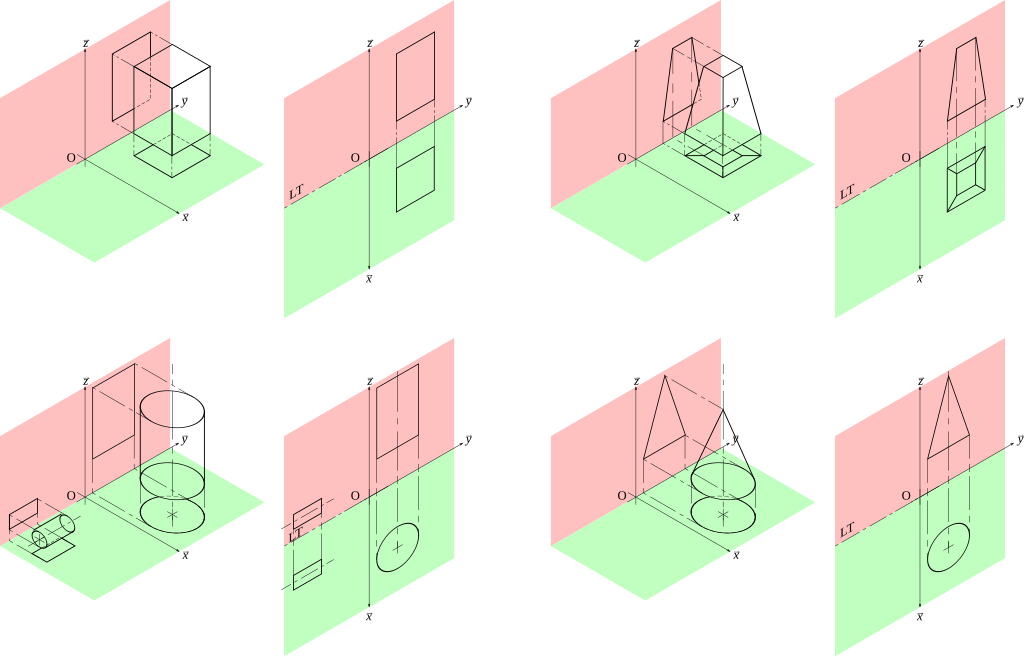
L’élément central de la géométrie du dessin est la projection rectangulaire, qui permet de représenter sans ambiguïté des objets tridimensionnels sur une surface plane. Cette technique permet de créer des dessins qui reflètent différentes vues d’un objet, que ce soit d’en haut, de face et de côté. Chaque projection montre différents aspects de la structure, ce qui permet de comprendre pleinement sa géométrie.
Les projections rectangulaires, par exemple, démontrent leur utilité dans la conception des bâtiments. Le plan d’un bâtiment explique la disposition des pièces et l’agencement des portes et des fenêtres, tandis que les projections verticales montrent la hauteur et les proportions de la façade. En outre, les projections latérales permettent d’analyser la profondeur et les détails de la structure, tels que les saillies de toit ou les détails de la façade.
Le dessin de la géométrie permet également de résoudre des problèmes spatiaux complexes, tels que l’interpénétration des solides. En architecture, l’exemple est utilisé pour illustrer les toits voûtés, ce qui permet de déterminer comment les différents éléments s’assemblent. En génie mécanique, ces techniques sont utilisées dans la conception de pièces de machines, dans lesquelles chaque composant doit s’emboîter parfaitement avec les autres.
L’une des principales caractéristiques du dessin géométrique est sa polyvalence. La méthode de projection permet de créer des images de figures géométriques simples et de formes complexes, telles que des surfaces ellipsoïdales ou hyperboloïdes. L’introduction de cette technique dans la pratique du design est due à la contribution inestimable de Gaspard Monge, qui a fait de la géométrie de dessin un outil alliant la précision mathématique à l’esthétique et à la fonctionnalité.
Grâce à la géométrie de dessin, il est également devenu possible de visualiser des concepts qui restaient auparavant dans le domaine de l’imagination. Ces techniques ne sont pas seulement un outil de création de dessins, mais aussi un outil d’analyse spatiale permettant de comprendre et d’optimiser les conceptions.
Applications et innovations de Gaspard Monge
L’une des réalisations les plus impressionnantes de Gaspard Monge a été l’application des principes de la géométrie du dessin à la résolution de problèmes pratiques de construction. Ses recherches ne se sont pas limitées à la création de modèles spatiaux théoriques, mais ont également porté sur des méthodes d’ingénierie spécifiques, telles que la stéréotomie, la science de la taille de la pierre, dont l’application aux voûtes et aux constructions sans mortier a révolutionné l’architecture du XVIIIe siècle.
Monge a noté qu’un élément clé d’une conception réussie est une bonne compréhension des lignes de courbure à la surface des objets. Ces lignes, une disposition orthogonale sur la surface, soulignent esthétiquement le caractère de l’objet et, surtout, facilitent la planification de la division des éléments structurels. Ces principes ont permis d’assembler des voûtes en pierre à partir d’éléments parfaitement adaptés les uns aux autres et de former des structures stables sans utiliser de mortier.
Les pierres sont taillées pour s’emboîter parfaitement, ce qui garantit leur durabilité et des effets visuels impressionnants.
L’attention de Monge ne s’est pas limitée aux structures architecturales. Ses analyses et méthodes ont été appliquées à l’ingénierie mécanique, alors que la précision de la conception est primordiale. La projection rectangulaire a été rapidement utilisée dans la conception de machines, ce qui a permis de définir avec précision les formes et les proportions des pièces individuelles et la manière dont elles s’assemblent.
Une autre avancée a été la combinaison de la géométrie de dessin et de l’esthétique. Monge estimait que les lignes de construction devaient refléter le caractère de la surface sur laquelle elles se trouvaient. Il a ainsi introduit une nouvelle qualité dans la conception architecturale, dans laquelle la forme et la fonctionnalité se complètent. Les lignes de séparation sur les voûtes ou les façades des bâtiments sont devenues un élément décoratif, donnant une apparence harmonieuse à l’ensemble.
Monge a montré que la géométrie du dessinateur n’est pas seulement un outil mathématique, mais un langage universel qui combine les fondements théoriques avec les besoins pratiques de la construction et de la conception. C’est pourquoi ses réalisations restent pertinentes et inspirent les générations successives de concepteurs.
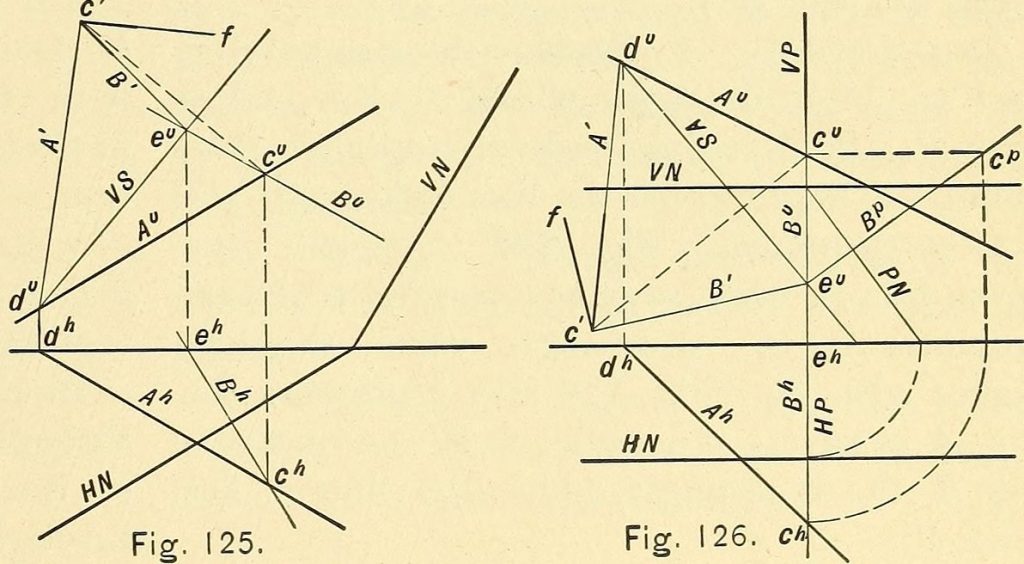
Critiques et influence de la géométrie de dessin
Malgré la nature révolutionnaire de la géométrie de dessin et ses applications polyvalentes, la théorie de Gaspard Monge n’était pas exempte de limites et a fait l’objet de critiques, en particulier dans le contexte de structures plus complexes. Le premier problème, et le plus important, était la difficulté d’appliquer les principes de la stéréotomie à des structures aux formes plus inhabituelles, comme les ponts diagonaux ou les voûtes aux surfaces non extensibles.
Les ponts construits en Europe au XIXe siècle, en particulier les structures conçues pour le passage des trains, sont un exemple de ces limitations. Dans le cas des ponts en diagonale, où l’angle entre la route et la voie ferrée est faible, la géométrie de dessin de Monge n’a pas toujours fourni les outils adéquats pour une répartition optimale des forces. Comme l’ont souligné les critiques, les lignes de courbure que Monge proposait comme élément clé de la conception ne correspondaient pas toujours aux exigences mécaniques réelles, telles que la répartition de la pression ou la résistance aux vibrations.
Bien que pleinement justifiées, ces critiques ne diminuent pas pour autant l’importance de Monge en tant que fondateur de la méthodologie de base de la géométrie spatiale. Son travail a inspiré des générations d’ingénieurs qui ont développé et adapté ses méthodes à de nouveaux défis techniques. Dans la seconde moitié du XIXe siècle, par exemple, les techniques de conception ont évolué avec le développement de la théorie de l’élasticité et de la science des matériaux, qui ont permis de mieux comprendre le comportement mécanique complexe des structures.
L’influence de Monge a également été évidente dans le développement ultérieur de l’architecture et de l’ingénierie au XXe siècle. À l’ère moderne, des structures telles que les coques en béton et les structures métalliques légères ont introduit des possibilités de conception entièrement nouvelles, tout en étant fondées sur les principes de base de la géométrie de dessin. Les idées de Monge, qui combinaient théorie et pratique, ont formé les fondations du développement de ces technologies innovantes.
Monge a également laissé une empreinte durable sur l’ enseignement technique. Son approche, qui met l’accent sur les applications pratiques de la géométrie, a été adoptée dans les écoles techniques du monde entier. Ses méthodes d’enseignement, basées sur une présentation claire de la relation entre les solides de l’espace et leurs projections, sont devenues la base de la formation des ingénieurs et des architectes.
En résumé, la critique de certains aspects de la théorie de Monge a été le point de départ du développement de la géométrie du dessin plutôt que sa négation. L’impact de son travail dépasse largement l’époque à laquelle il a vécu, et ses méthodes restent un élément clé de l’ingénierie et de l’architecture modernes. Monge a montré que la pensée géométrique peut être un outil d’analyse et une source d’innovation qui change le monde.

Géométrie descriptive – Résumé
La géométrie descriptive de Gaspard Monge a constitué une étape fondamentale dans l’organisation de la pensée spatiale. Elle associe la précision des mathématiques aux exigences pratiques de l’architecture et de l’ingénierie. L’introduction de projections rectangulaires pour représenter la réalité tridimensionnelle sur un plan bidimensionnel a changé la façon dont les gens concevaient et comprenaient les structures.
Malgré les critiques et les remises en cause ultérieures de certaines conceptions plus complexes, Monge a posé des bases qui ont été développées et affinées au cours des siècles suivants. La géométrie descriptive est devenue un outil universel, un langage de conception qui est encore enseigné aujourd’hui aux ingénieurs et aux architectes. L’idée de combiner fonctionnalité et esthétique dans la conception spatiale a pris une nouvelle dimension grâce à Monge. Son héritage reste évident dans tous les travaux qui impliquent une réflexion sur l’espace.