O que é a geometria descritiva?
Índice
Desde o início dos tempos, a humanidade tem procurado formas de representar com exatidão o espaço de uma forma compreensível e ordenada. Embora os desenhos ou diagramas simples tenham sido suficientes para o ser humano na antiguidade, foi só com o trabalho de Gaspard Monge, no século XVIII, que estes esforços adquiriram exatidão matemática e universalidade. Na sua essência, a geometria descritiva é a ciência da projeção de objetos espaciais em planos bidimensionais de uma forma precisa e inequívoca.
Qual é a base da geometria descritiva?
A ideia central da geometria descritiva é que as projeções sobre planos podem representar sólidos tridimensionais complexos. Isto permite a análise da sua estrutura e relações espaciais, mantendo-se no domínio dos desenhos bidimensionais. Esta abordagem é extremamente importante na engenharia e na arquitetura, onde costuma ser indispensável planear com precisão a estrutura de um edifício ou máquina antes de proceder à sua implementação.
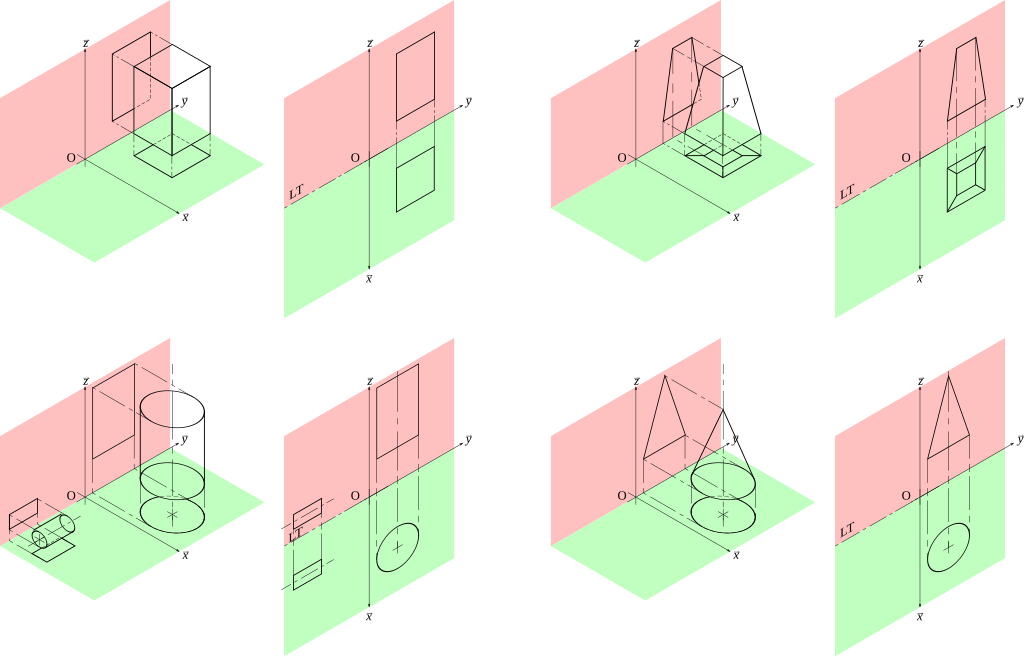
A geometria descritiva proporciona uma forma fácil de compreender o espaço. Graças à projeção retangular uma das técnicas básicas deste campo –, é possível olhar para um sólido de diferentes perspetivas, tornando este método uma ferramenta extremamente versátil. Uma imagem vista de cima (projeção horizontal), de lado (projeção lateral) ou de frente (projeção vertical) capta muita informação sobre um objeto que pode ser analisada num contexto de design.
A sua vantagem é a capacidade de combinar a matemática teórica com aplicações práticas. A conceção de edifícios, pontes ou máquinas baseia-se na capacidade de prever como os vários elementos irão interagir na realidade. Graças aos métodos de Monge, os engenheiros conseguiam planear e resolver problemas de construção antes mesmo do início dos trabalhos no local de construção.
Génese e desenvolvimento da disciplina
Embora seja atualmente considerada um ramo fundamental da matemática aplicada, a geometria descritiva deve as suas origens às necessidades práticas. No século XVIII, quando Gaspard Monge iniciou a sua carreira de jovem engenheiro militar, Monge deparou-se com um problema que exigia uma modelação rigorosa do espaço no âmbito da conceção de fortificações. Os princípios de construção destas estruturas exigiam uma grande exatidão e tinham de ter paredes e abóbadas à prova de bomba.
Aos 18 anos, Monge já tinha desenvolvido as bases de um sistema que permitia representar objetos tridimensionais complexos em duas dimensões. No entanto, devido à importância estratégica deste conhecimento, as suas descobertas foram classificadas como segredo militar e não foram disponibilizadas ao público durante muitos anos. Foi só em 1794, após a Revolução Francesa, que Monge partilhou os seus conhecimentos, introduzindo a geometria de escoamento no currículo da École Normale e da recém-fundada École Polytechnique.
A introdução da geometria de traçado no ensino da École Polytechnique em 1795 foi um acontecimento marcante. Além das suas excelentes competências matemáticas, Monge tinha o dom de comunicar ideias complexas de uma forma compreensível e inspiradora. Já nas suas primeiras aulas, o novo domínio despertou grande interesse entre os estudantes e tornou-se a base da ciência técnica.
Monge definiu a geometria de desenhador como uma ferramenta com dois objetivos principais: em primeiro lugar, permitir a representação precisa de objetos tridimensionais em duas dimensões e, em segundo lugar, tirar conclusões sobre as formas e as relações entre esses objetos. Graças a estes princípios, o novo domínio ganhou dimensões teóricas e práticas, o que permitiu a sua rápida difusão.

Conceitos básicos da geometria de projeto
O elemento central da geometria de projeto são as projeções retangulares, que permitem representar objetos tridimensionais numa superfície plana de forma inequívoca. Esta técnica permite criar desenhos que refletem diferentes vistas de um objeto: de cima, de frente e de lado. Cada projeção mostra vários aspetos da estrutura, permitindo uma compreensão completa da sua geometria.
As projeções retangulares, por exemplo, demonstram a sua utilidade prática no desenho de edifícios. A planta de um edifício mostra a disposição das divisões e a disposição das portas e janelas, enquanto as projeções verticais mostram a altura e as proporções da fachada. Além disso, as projeções laterais permitem analisar a profundidade e os detalhes da estrutura, como as saliências do telhado ou os pormenores da fachada.
A geometria do desenho também permite resolver problemas espaciais complexos, como a interpenetração de sólidos. Na arquitetura, o exemplo é utilizado para ilustrar telhados abobadados, ajudando a determinar a forma como os vários elementos se conjugam. Em engenharia mecânica, estas técnicas são utilizadas na conceção de peças de máquinas, em que cada componente deve encaixar perfeitamente com os outros.
Uma das principais caraterísticas da geometria de projeto é a sua versatilidade. O método de projeção permite criar imagens tanto de figuras geométricas simples como de formas complexas, como superfícies elipsoidais ou hiperbolóides. A introdução desta técnica na prática do design foi a contribuição inestimável de Gaspard Monge, que transformou a geometria de projeto numa ferramenta que combina precisão matemática com estética e funcionalidade.
Graças à geometria de projeto, também se tornou possível visualizar conceitos que anteriormente permaneciam no domínio da imaginação. Estas técnicas não são apenas uma ferramenta para criar desenhos, mas também uma ferramenta de análise espacial para compreender e otimizar os projetos.
As aplicações e inovações de Monge
Uma das realizações mais impressionantes de Gaspard Monge foi a aplicação dos princípios da geometria de projeto à solução de problemas práticos de construção. A sua investigação não se limitou à criação de modelos espaciais teóricos, mas incluiu também métodos de engenharia específicos, como a estereotomia – a ciência do corte da pedra, cuja aplicação à abóbada e à construção sem argamassa revolucionou a arquitetura do século XVIII.
Monge observou que um elemento-chave para o sucesso do design é a compreensão adequada das linhas de curvatura na superfície dos objetos. Estas linhas, uma disposição ortogonal na superfície, dão ênfase estética ao seu caráter e, mais importante ainda, facilitam o planeamento da divisão dos elementos estruturais. Estes princípios permitiram que as abóbadas de pedra fossem montadas a partir de elementos precisamente combinados que formavam estruturas estáveis sem utilizar argamassa.
A inovação de Monge não se limitou às estruturas arquitetónicas. Os seus métodos também foram aplicados na engenharia mecânica, onde a precisão do projeto é um aspeto essencial. A projeção retangular foi utilizada na conceção de máquinas, permitindo a definição precisa das formas e proporções das peças individuais e da forma como estas se encaixam.
Outro avanço foi a combinação da geometria de desenho com a estética. Monge acreditava que as linhas de construção deviam refletir o caráter da superfície em que se encontravam. Com isto, introduziu uma nova qualidade no desenho arquitetónico, em que a forma e a funcionalidade se complementam. As linhas divisórias em abóbadas ou fachadas de edifícios tornaram-se um elemento decorativo, dando uma aparência harmoniosa ao conjunto.
Monge demonstrou que a geometria do desenhador não é apenas uma ferramenta matemática, mas uma linguagem universal que combina os fundamentos teóricos com as necessidades práticas da construção e do projeto. Como resultado, as suas realizações permanecem relevantes e inspiram sucessivas gerações de desenhadores.
Críticas e influência da geometria de projeto
Apesar do caráter revolucionário da geometria de projeto e da sua versatilidade de aplicações, a teoria de Gaspard Monge não estava isenta de limitações e enfrentou críticas, especialmente no contexto de estruturas mais complexas. O primeiro e mais proeminente problema foi a dificuldade de aplicar os princípios da estereotomia a estruturas com formas mais invulgares, como pontes diagonais ou abóbadas com superfícies não expansíveis.
Um exemplo destas limitações foi as pontes construídas na Europa no século XIX, nomeadamente as estruturas destinadas à passagem de comboios. No caso das pontes diagonais, em que o ângulo entre a estrada e a via-férrea era pequeno, a geometria de projeto de Monge nem sempre fornecia ferramentas adequadas para uma distribuição ótima das forças. Como os críticos salientaram, as linhas de curvatura que Monge propôs como elemento-chave do projeto nem sempre correspondiam a requisitos mecânicos reais, como a distribuição de pressões ou a resistência às vibrações.
Embora plenamente justificadas, estas críticas não diminuem a importância de Monge como o fundador da metodologia básica da geometria espacial. O seu trabalho inspirou gerações de engenheiros que desenvolveram e adaptaram os seus métodos a novos desafios técnicos. Na segunda metade do século XIX, por exemplo, as técnicas de projeto evoluíram com o desenvolvimento da teoria da elasticidade e da ciência dos materiais, o que permitiu uma melhor compreensão do complexo comportamento mecânico das estruturas.
A influência de Monge também foi evidente no desenvolvimento posterior da arquitetura e da engenharia no século XX. Na era moderna, estruturas como as cascas de betão e as estruturas de aço leve introduziram possibilidades de conceção inteiramente novas, mas ao mesmo tempo baseavam-se nos princípios básicos da geometria de projeto. As ideias de Monge, combinando teoria e prática, foram a base para o desenvolvimento destas tecnologias inovadoras.
Monge também deixou uma marca duradoura no ensino técnico. A sua abordagem, que dá ênfase às aplicações práticas da geometria, foi adotada em escolas técnicas de todo o mundo. Os seus métodos de ensino, baseados numa apresentação clara da relação entre os sólidos espaciais e as suas projeções, serviram de base à formação de engenheiros e arquitetos.
Em suma, as críticas a alguns aspetos da teoria de Monge foram um ponto de partida para o desenvolvimento da geometria de projeto e não a sua negação. O impacto do seu trabalho estende-se muito para além da época em que viveu, e os seus métodos continuam a ser um elemento-chave da engenharia e da arquitetura modernas. Monge mostrou que o pensamento geométrico pode ser uma ferramenta de análise e uma fonte de inovação que muda o mundo.

Geometria descritiva – resumo
A geometria descritiva de Gaspard Monge foi um passo fundamental para a organização do pensamento espacial. Combinou a precisão da matemática com os requisitos práticos da arquitetura e da engenharia. A introdução de projeções retangulares para representar a realidade tridimensional num plano bidimensional mudou a forma como as pessoas concebiam e compreendiam as estruturas.
Apesar das críticas e desafios posteriores a projetos mais complexos, Monge lançou uma base desenvolvida e aperfeiçoada ao longo dos séculos seguintes. A geometria descritiva tornou-se uma ferramenta universal, uma linguagem de desenho que ainda hoje é ensinada por engenheiros e arquitetos. A ideia de combinar funcionalidade e estética na conceção de espaços ganhou uma nova dimensão graças a Monge. O seu legado permanece evidente em qualquer trabalho que envolva o pensamento espacial.