Che cos’è la geometria descrittiva?
Indice dei contenuti
Fin dalla notte dei tempi, l’umanità ha cercato un modo per rappresentare accuratamente lo spazio in modo comprensibile e ordinato. Anche se semplici disegni o diagrammi sono serviti all’uomo fin dall’antichità, è stato solo grazie al lavoro di Gaspard Monge nel XVIII secolo che questi sforzi hanno ottenuto precisione matematica e universalità. La geometria descrittiva è la scienza della proiezione di oggetti spaziali su piani bidimensionali in modo preciso e non ambiguo.
Quali sono le basi della geometria descrittiva?
L’idea centrale della geometria descrittiva è che le proiezioni sui piani possono rappresentare solidi tridimensionali complessi. Ciò consente di analizzare la loro struttura e le relazioni spaziali, pur rimanendo nell’ambito dei disegni bidimensionali. Questo approccio è di grande importanza in ingegneria e architettura, dove spesso è fondamentale pianificare con precisione la struttura di un edificio o di una macchina prima di procedere alla sua realizzazione.
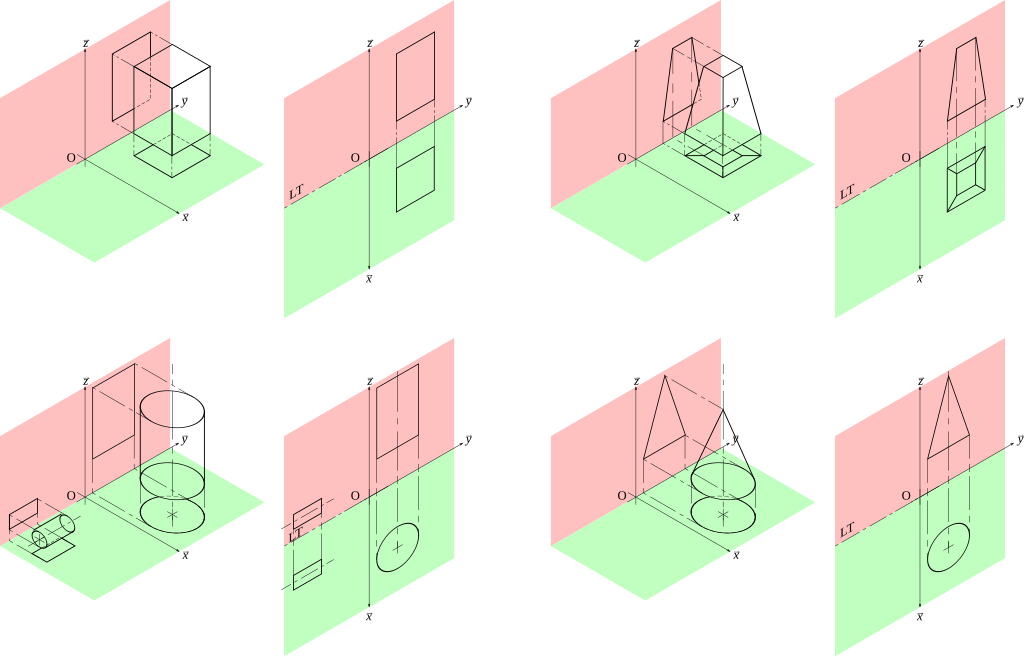
La geometria descrittiva offre un modo semplice per comprendere lo spazio. Grazie alla proiezione rettangolare, una delle tecniche di base di questo campo, è possibile osservare un solido da diverse prospettive, rendendo questo metodo uno strumento estremamente versatile. Un’immagine vista dall’alto (proiezione orizzontale), di lato (proiezione laterale) o di fronte (proiezione verticale) cattura molte informazioni su un oggetto che possono essere analizzate in un contesto progettuale.
Il suo vantaggio è la capacità di combinare la matematica teorica con le applicazioni pratiche. La progettazione di edifici, ponti o macchinari si basa sulla capacità di prevedere come i vari elementi interagiranno nella realtà. Grazie ai metodi di Monge, gli ingegneri hanno potuto pianificare e risolvere i problemi di costruzione prima ancora di iniziare i lavori in cantiere.
Genesi e sviluppo della disciplina
Sebbene oggi sia considerata una branca fondamentale della matematica applicata, la geometria descrittiva deve le sue origini a esigenze pratiche. Nel XVIII secolo, quando Gaspard Monge iniziò la sua carriera di giovane ingegnere militare, si imbatté in un problema che richiedeva una modellazione rigorosa dello spazio nel contesto della progettazione di fortificazioni. I principi costruttivi di queste strutture richiedevano una grande precisione e dovevano avere mura e volte a prova di bomba.
All’età di 18 anni, Monge aveva già sviluppato le basi di un sistema che permetteva di rappresentare in due dimensioni oggetti tridimensionali complessi; tuttavia, a causa dell’importanza strategica di queste conoscenze, le sue scoperte furono considerate un segreto militare e non vennero rese pubbliche per molti anni. Solo nel 1794, dopo la Rivoluzione francese, Monge condivise le sue conoscenze, introducendo il disegno tecnico nel curriculum dell’École Normale e della neonata École Polytechnique.
L’introduzione della disciplina nell’insegnamento all’École Polytechnique nel 1795 fu un evento epocale. Oltre alle sue eccellenti capacità matematiche, Monge aveva il dono di comunicare idee complesse in modo comprensibile e stimolante. Già durante le sue prime lezioni, il nuovo campo suscitò grande interesse tra gli studenti e divenne la base della scienza tecnica.
Monge definì la geometria del disegno tecnico come uno strumento con due obiettivi principali: in primo luogo, consentire la rappresentazione precisa di oggetti tridimensionali in due dimensioni, in secondo luogo, trarre conclusioni sulle forme e sulle relazioni tra questi oggetti. Grazie a questi principi, il nuovo campo acquisì dimensioni teoriche e pratiche che ne permisero una rapida diffusione.

Concetti di base della geometria del disegno
L’elemento centrale della geometria del disegno è costituito dalle proiezioni rettangolari, che consentono di rappresentare gli oggetti tridimensionali su una superficie piana in modo univoco. Questa tecnica consente di creare disegni che riflettono diverse prospettive di un oggetto: dall’alto, dal davanti e di lato. Ogni proiezione mostra vari aspetti della struttura, consentendo così di avere piena comprensione della sua geometria.
Le proiezioni rettangolari, ad esempio, dimostrano la loro praticità nella progettazione degli edifici. La pianta di un edificio mostra la disposizione delle stanze e la disposizione di porte e finestre, mentre le proiezioni verticali mostrano l’altezza e le proporzioni della facciata. Inoltre, le proiezioni laterali consentono di analizzare la profondità e i dettagli della struttura, come le sporgenze del tetto o i particolari della facciata.
La geometria del disegno permette anche di risolvere problemi spaziali complessi, come la compenetrazione di solidi. In architettura, l’esempio viene utilizzato per illustrare i tetti a volta, aiutando a determinare come i vari elementi si uniscono. In ingegneria meccanica, queste tecniche sono utilizzate nella progettazione di parti di macchine, dove ogni componente deve adattarsi perfettamente agli altri.
Una caratteristica fondamentale della geometria di disegno è la sua versatilità. Il metodo di proiezione permette di creare immagini sia di figure geometriche semplici sia di forme complesse, come superfici ellissoidali o iperboloidi. L’introduzione di questa tecnica nella progettazione è stato il prezioso contributo di Gaspard Monge, che ha trasformato la geometria disegnata in uno strumento che unisce la precisione matematica all’estetica e alla funzionalità.
Grazie ad essa, è diventato possibile visualizzare concetti che prima rimanevano nel regno dell’immaginazione. Queste tecniche non sono solo uno strumento per creare disegni, ma anche uno strumento di analisi spaziale per comprendere e ottimizzare i progetti.
Applicazioni e innovazioni di Monge
Uno dei risultati più impressionanti di Gaspard Monge fu l’applicazione dei principi della geometria del disegno alla soluzione di problemi pratici di costruzione. La sua ricerca non si limitava alla creazione di modelli spaziali teorici, ma comprendeva anche metodi ingegneristici specifici, come la stereotomia, la scienza del taglio della pietra, la cui applicazione alle volte e alle costruzioni senza malta rivoluzionò l’architettura del XVIII secolo.
Monge osservò che un elemento chiave per il successo della progettazione è la corretta comprensione delle linee di curvatura sulla superficie degli oggetti. Queste linee, una disposizione ortogonale sulla superficie, forniscono un’enfasi estetica sul suo carattere e, soprattutto, facilitano la pianificazione della divisione degli elementi strutturali. Questi principi permisero di assemblare le volte in pietra con elementi abbinati con precisione, formando strutture stabili senza l’uso di malta.
L’innovazione di Monge non si limitò alle strutture architettoniche. I suoi metodi furono applicati anche nell’ingegneria meccanica, dove l’accuratezza della progettazione è fondamentale. La proiezione rettangolare venne utilizzata nella progettazione di macchine, consentendo di definire con precisione le forme e le proporzioni delle singole parti e il modo in cui si incastrano tra loro.
Un’altra svolta fu la combinazione di geometria di disegno ed estetica. Monge riteneva che le linee di costruzione dovessero riflettere il carattere della superficie su cui si trovavano. In questo modo, introdusse una nuova qualità nella progettazione architettonica, in cui forma e funzionalità si completavano a vicenda. Le linee di divisione delle volte o delle facciate degli edifici diventano un elemento decorativo, che conferisce un aspetto armonioso all’insieme.
Monge dimostrò che la geometria del disegnatore non è solo uno strumento matematico, bensì un linguaggio universale che unisce i fondamenti teorici alle esigenze pratiche della costruzione e della progettazione. Di conseguenza, i suoi risultati rimangono attuali ancor oggi e ispirano le prossime generazioni di progettisti.
Critiche e influenza della geometria del disegno
Nonostante la natura rivoluzionaria della geometria del disegno e le sue versatili applicazioni, la teoria di Gaspard Monge non era esente da limitazioni e dovette affrontare critiche, soprattutto nel contesto di strutture più complesse. Il primo e più evidente problema era la difficoltà di applicare i principi della stereotomia a strutture dalle forme più insolite, come ponti diagonali o volte con superfici non espandibili.
Un esempio di queste limitazioni sono i ponti costruiti in Europa nel XIX secolo, in particolare le strutture progettate per il passaggio dei treni. Nel caso dei ponti diagonali, dove l’angolo tra la strada e la ferrovia era lieve, la geometria di Monge non sempre forniva strumenti adeguati per una distribuzione ottimale delle forze. Come sottolineato dai critici, le linee di curvatura proposte da Monge come elemento chiave della progettazione non sempre corrispondevano ai reali requisiti meccanici, come la distribuzione della pressione o la resistenza alle vibrazioni.
Pur essendo pienamente giustificate, queste critiche non sminuiscono l’importanza di Monge come fondatore della metodologia di base della geometria spaziale. Il suo lavoro ha ispirato generazioni di ingegneri che hanno sviluppato e adattato i suoi metodi alle nuove sfide tecniche. Nella seconda metà del XIX secolo, ad esempio, le tecniche di progettazione si evolvettero con lo sviluppo della teoria dell’elasticità e della scienza dei materiali, traducendosi in una migliore comprensione del complesso comportamento meccanico delle strutture.
L’influenza di Monge è evidente anche nello sviluppo successivo dell’architettura e dell’ingegneria nel XX secolo. Nell’era moderna, strutture come i gusci di cemento e le strutture leggere in acciaio hanno introdotto possibilità di progettazione completamente nuove, ma allo stesso tempo si basavano sui principi fondamentali della geometria redazionale. Le idee di Monge, che combinano teoria e pratica, furono la base per lo sviluppo di queste tecnologie innovative.
Monge ha anche lasciato un segno duraturo nell’istruzione tecnica. Il suo approccio, che enfatizza le applicazioni pratiche della geometria, è stato adottato nelle scuole tecniche di tutto il mondo. I suoi metodi di insegnamento, basati su una chiara presentazione della relazione tra i solidi spaziali e le loro proiezioni, sono diventati la base per la formazione di ingegneri e architetti.
In sintesi, le critiche rivolte ad alcuni aspetti della teoria di Monge sono state un punto di partenza per l’ulteriore sviluppo della geometria redazionale, piuttosto che la sua negazione. L’impatto del suo lavoro va ben oltre l’epoca in cui visse e i suoi metodi rimangono un elemento chiave dell’ingegneria e dell’architettura moderne. Monge ha dimostrato che il pensiero geometrico può essere uno strumento di analisi e una fonte di innovazione che cambia il mondo.

Geometria descrittiva – Sintesi
La geometria descrittiva di Gaspard Monge fu un passo fondamentale verso l’organizzazione del pensiero spaziale. Essa combinava la precisione della matematica con le esigenze pratiche dell’architettura e dell’ingegneria. L’introduzione di proiezioni rettangolari per rappresentare la realtà tridimensionale su un piano bidimensionale cambiò il modo di progettare e comprendere le strutture.
Nonostante le critiche e le sfide successive a progetti più complessi, Monge gettò le basi che furono sviluppate e perfezionate nei secoli successivi. La geometria descrittiva divenne uno strumento universale, un linguaggio di progettazione che viene insegnato ancora oggi da ingegneri e architetti. L’idea di combinare funzionalità ed estetica nella progettazione degli spazi ha acquisito una nuova dimensione grazie a Monge. La sua eredità rimane evidente in qualsiasi opera che coinvolga il pensiero spaziale.