Co je deskriptivní geometrie?
Obsah
Od počátku věků lidstvo hledalo způsoby, jak přesně a srozumitelně znázornit prostor. Ačkoli jednoduché nákresy nebo diagramy sloužily lidem již od starověku, teprve práce Gasparda Mongeho v 18. století dodaly těmto snahám matematickou přesnost a univerzálnost. Ve své podstatě je deskriptivní geometrie vědou o přesném a jednoznačném promítání prostorových objektů do dvourozměrných rovin.
Co je základem deskriptivní geometrie?
Ústřední myšlenkou deskriptivní geometrie je, že projekce na roviny mohou znázorňovat složitá trojrozměrná tělesa. To umožňuje analyzovat jejich strukturu a prostorové vztahy, a přitom zůstat v oblasti dvourozměrných nákresů. Tento přístup má velký význam ve strojírenství a architektuře, kde je často velmi důležité přesně naplánovat konstrukci budovy nebo stroje předtím, než se přistoupí k její realizaci.
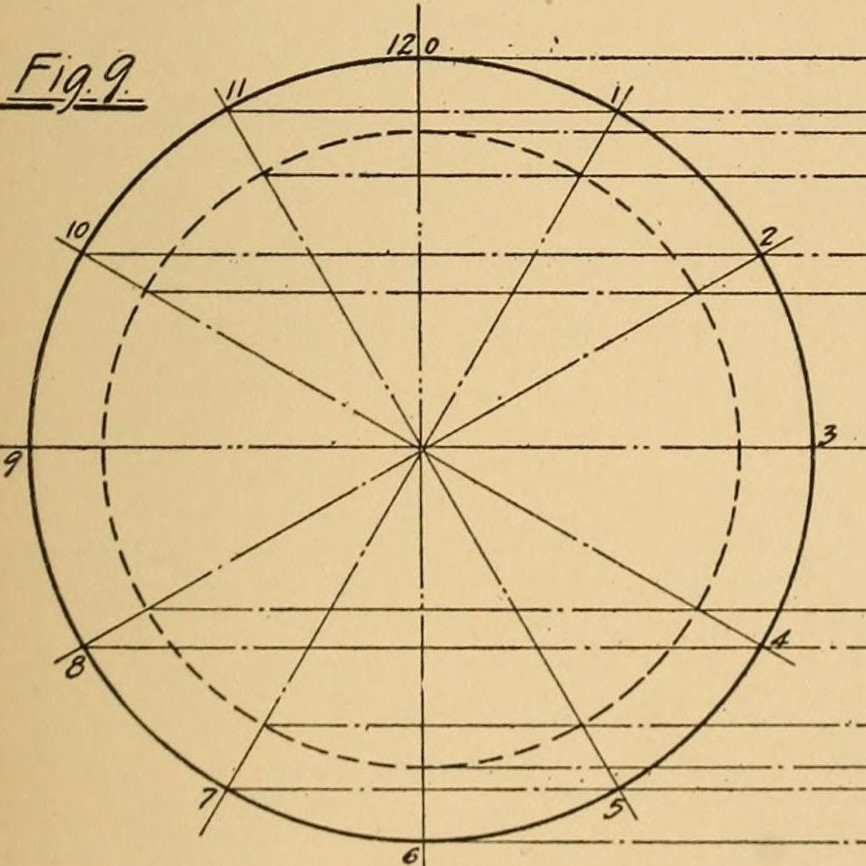
Deskriptivní geometrie poskytuje snadný způsob, jak porozumět prostoru. Díky pravoúhlému promítání – jedné ze základních technik tohoto oboru – je možné nahlížet na těleso z různých perspektiv, což z této metody činí mimořádně univerzální nástroj. Obraz viděný shora (horizontální projekce), z boku (boční projekce) nebo zepředu (vertikální projekce) zachycuje mnoho informací o objektu, které lze analyzovat v kontextu návrhu.
Jeho výhodou je schopnost spojit teoretickou matematiku s praktickými aplikacemi. Návrh budov, mostů nebo strojních zařízení je založen na schopnosti předvídat, jak budou jednotlivé prvky ve skutečnosti vzájemně působit. Díky Mongeovým metodám mohli inženýři plánovat a řešit konstrukční problémy ještě před zahájením prací na stavbě.
Geneze a vývoj oboru
Ačkoli je dnes deskriptivní geometrie považována za základní obor aplikované matematiky, za svůj vznik vděčí praktickým potřebám. Když Gaspard Monge v 18. století začínal svou kariéru jako mladý vojenský inženýr, narazil v souvislosti s projektováním opevnění na problém vyžadující důsledné modelování prostoru. Konstrukční zásady takových staveb vyžadovaly velkou přesnost a musely mít stěny a klenby odolné proti bombám.
Ve svých 18 letech již Monge vyvinul základy systému, který umožňoval znázornit složité trojrozměrné objekty ve dvou rozměrech. Vzhledem ke strategickému významu těchto poznatků však byly jeho objevy považovány za vojenské tajemství a po mnoho let nebyly zpřístupněny veřejnosti. Teprve po Francouzské revoluci v roce 1794 se Monge podělil o své poznatky a zavedl drenážní geometrii do učebních osnov na École Normale a nově založené École Polytechnique.
Zavedení rýsovací geometrie do výuky na École Polytechnique v roce 1795 bylo přelomovou událostí. Kromě vynikajících matematických schopností měl Monge dar srozumitelně a inspirativně předávat složité myšlenky. Již během jeho prvních přednášek vzbudil nový obor mezi studenty velký zájem a stal se základem technické vědy.
Monge definoval rýsovací geometrii jako nástroj se dvěma hlavními cíli: zaprvé umožnit přesné zobrazení trojrozměrných objektů ve dvou rozměrech, zadruhé vyvozovat závěry o tvarech a vztazích mezi těmito objekty. Díky těmto principům získal nový obor teoretické i praktické rozměry, což umožnilo jeho rychlé rozšíření.

Základní pojmy rýsovací geometrie
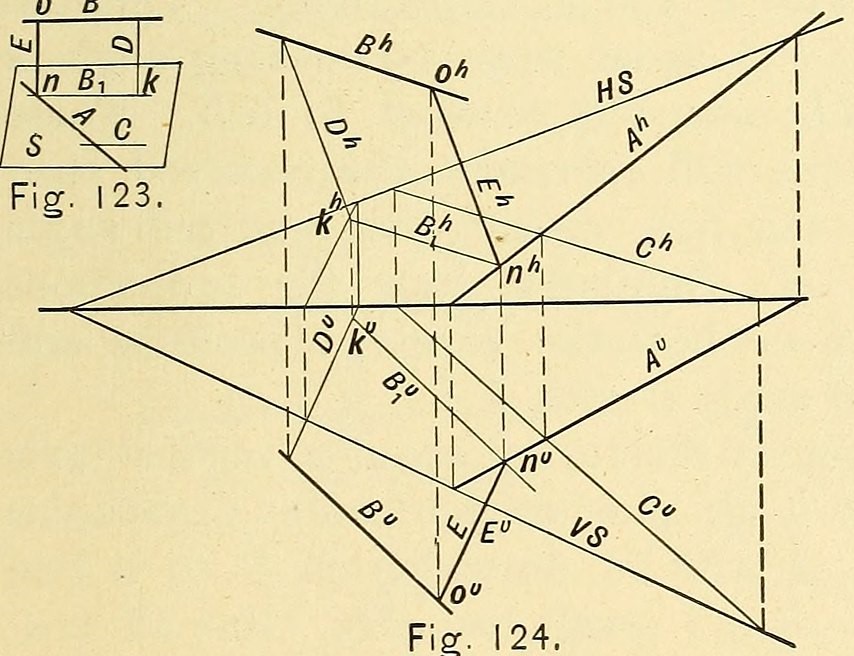
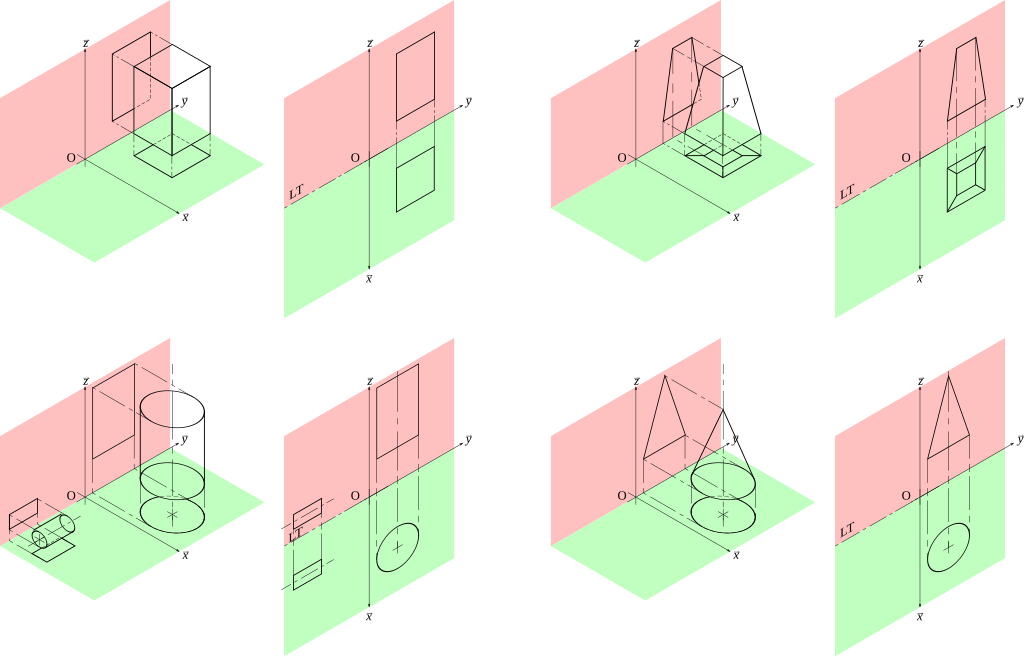
Ústředním prvkem rýsovací geometrie jsou pravoúhlé průměty, které umožňují jednoznačné zobrazení trojrozměrných objektů na rovné ploše. Tato technika umožňuje vytvářet výkresy, které odrážejí různé pohledy na objekt: shora, zepředu a ze strany. Každá projekce zobrazuje různé aspekty konstrukce, což umožňuje plně pochopit její geometrii.
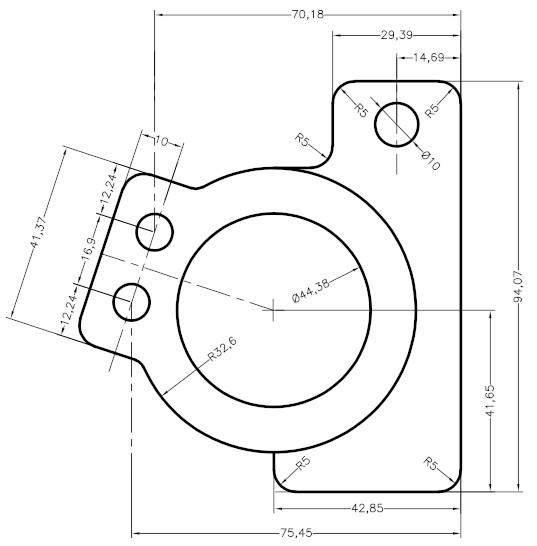
Například pravoúhlé projekce ukazují jejich praktičnost při navrhování budov. Půdorys budovy ukazuje rozložení místností a rozmístění dveří a oken, zatímco svislé projekce ukazují výšku a proporce fasády. Boční průměty navíc umožňují analyzovat hloubku a detaily stavby, jako jsou střešní výstupky nebo detaily fasády.
Kreslení geometrie také umožňuje řešit složité prostorové problémy, jako je například průnik těles. V architektuře se tento příklad používá pro znázornění klenutých střech a pomáhá určit, jak se jednotlivé prvky spojují. Ve strojírenství se tyto techniky používají při navrhování strojních součástí, kde každá součást musí dokonale zapadat do ostatních.
Klíčovým rysem kreslení geometrie je její univerzálnost. Metoda promítání umožňuje vytvářet obrazy jednoduchých geometrických útvarů i složitých tvarů, jako jsou elipsoidické nebo hyperboloidní plochy. O zavedení této techniky do konstrukční praxe se neocenitelně zasloužil Gaspard Monge, který z rýsovací geometrie vytvořil nástroj, který spojuje matematickou přesnost s estetikou a funkčností.
Díky rýsovací geometrii bylo také možné vizualizovat koncepty, které dříve zůstávaly v oblasti představivosti. Tyto techniky jsou nejen nástrojem pro tvorbu výkresů, ale také nástrojem prostorové analýzy pro pochopení a optimalizaci návrhů.
Aplikace a inovace společnosti Monge
Jedním z nejpůsobivějších úspěchů Gasparda Mongeho bylo uplatnění principů rýsovací geometrie při řešení praktických stavebních problémů. Jeho výzkum se neomezoval pouze na tvorbu teoretických prostorových modelů, ale zahrnoval i specifické inženýrské metody, například stereotomii – nauku o řezání kamene, jejíž aplikace na klenby a bezmaltové konstrukce způsobila v architektuře 18. století revoluci.
Monge si všiml, že klíčovým prvkem úspěšného návrhu je správné pochopení linií zakřivení na povrchu objektů. Tyto linie, ortogonální uspořádání na povrchu, poskytují estetické zdůraznění jeho charakteru, a především usnadňují plánování členění konstrukčních prvků. Tyto zásady umožnily sestavit kamenné klenby z přesně sladěných prvků, které tvořily stabilní struktury bez použití malty.
Mongeova inovace se neomezovala pouze na architektonické stavby. Jeho metody se uplatnily také ve strojírenství, kde je přesnost návrhu klíčová. Při konstrukci strojů se používalo pravoúhlé promítání, které umožňovalo přesně definovat tvary a proporce jednotlivých dílů a jejich vzájemné spojení.
Dalším průlomem bylo spojení kreslící geometrie a estetiky. Monge věřil, že konstrukční linie by měly odrážet charakter povrchu, na kterém se nacházejí. Tím vnesl do architektonického navrhování novou kvalitu, kdy se forma a funkčnost vzájemně doplňují. Dělící linie na klenbách nebo fasádách budov se staly dekorativním prvkem, který dodával celku harmonický vzhled.
Monge ukázal, že kreslířská geometrie není jen matematickým nástrojem, ale univerzálním jazykem, který spojuje teoretické základy s praktickými potřebami stavby a designu. Díky tomu jsou jeho úspěchy stále aktuální a inspirují další generace projektantů.
Kritika a vliv rýsovací geometrie
Navzdory revoluční povaze rýsovací geometrie a jejímu všestrannému využití nebyla teorie Gasparda Mongeho prosta omezení a čelila kritice, zejména v souvislosti se složitějšími konstrukcemi. Prvním a nejvýraznějším problémem byla obtížnost aplikace principů stereotomie na konstrukce neobvyklejších tvarů, jako jsou diagonální mosty nebo klenby s nerozšiřitelnými plochami.
Jedním z příkladů těchto omezení byly mosty stavěné v Evropě v 19. století, zejména konstrukce určené pro průjezd vlaků. V případě diagonálních mostů, kde byl úhel mezi silnicí a železnicí malý, neposkytovala Mongeova rýsovací geometrie vždy vhodné nástroje pro optimální rozložení sil. Jak upozorňovali kritici, linie zakřivení, které Monge navrhoval jako klíčový konstrukční prvek, ne vždy odpovídaly skutečným mechanickým požadavkům, jako je rozložení tlaku nebo odolnost proti vibracím.
Ačkoli je tato kritika plně oprávněná, nesnižuje význam Mongeho jako zakladatele základní metodologie prostorové geometrie. Jeho práce inspirovala generace inženýrů, kteří jeho metody rozvíjeli a přizpůsobovali novým technickým výzvám. Ve druhé polovině 19. století se například konstrukční techniky vyvíjely spolu s rozvojem teorie pružnosti a nauky o materiálech, což umožnilo lépe pochopit složité mechanické chování konstrukcí.
Mongeův vliv se projevil i v pozdějším vývoji architektury a inženýrství ve 20. století. V moderní éře konstrukce, jako jsou betonové skořepiny a lehké ocelové konstrukce, přinesly zcela nové konstrukční možnosti, ale zároveň vycházely ze základních principů rýsovací geometrie. Mongeovy myšlenky, spojující teorii a praxi, byly základem pro rozvoj těchto inovativních technologií.
Monge také zanechal trvalou stopu v technickém vzdělávání. Jeho přístup, který klade důraz na praktické využití geometrie, byl přijat na technických školách po celém světě. Jeho výukové metody, založené na jasném zobrazení vztahů mezi prostorovými tělesy a jejich průměty, se staly základem pro vzdělávání inženýrů a architektů.
Lze shrnout, že kritika, které čelily některé aspekty Mongeovy teorie, byla spíše východiskem pro další rozvoj rýsovací geometrie než jejím popřením. Vliv jeho díla dalece přesahuje dobu, ve které žil, a jeho metody zůstávají klíčovým prvkem moderního inženýrství a architektury. Monge ukázal, že geometrické myšlení může být nástrojem analýzy a zdrojem inovací, které mění svět.

Deskriptivní geometrie – shrnutí
Deskriptivní geometrie Gasparda Mongeho byla zásadním krokem k uspořádání prostorového myšlení. Spojovala přesnost matematiky s praktickými požadavky architektury a inženýrství. Zavedení pravoúhlých projekcí pro zobrazení trojrozměrné reality na dvourozměrné rovině změnilo způsob, jakým lidé navrhovali a chápali stavby.
Navzdory pozdější kritice a zpochybňování složitějších návrhů položil Monge základ, který se v následujících staletích rozvíjel a zdokonaloval. Deskriptivní geometrie se stala univerzálním nástrojem, konstrukčním jazykem, který se dodnes učí inženýři i architekti. Myšlenka spojení funkčnosti s estetikou v prostorovém navrhování získala díky Mongeovi nový rozměr. Jeho odkaz zůstává patrný v každé práci, která zahrnuje prostorové myšlení.